Тема: "Дифференциальные уравнения высших порядков, допускающие понижение порядка"
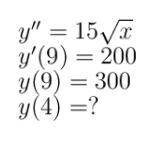
Другие вопросы по теме Математика
Популярные вопросы
- X6 3(x²+3y)4x2-(2x-1)(0,2x2+5y)(2a+b)2-(a-2b)(3x2-2,5y)(a-2)(a+2)(a +4(7x29+3xy?)(a2-5)(22+5)10...
1 - Определите правильные/неправильные предложения...
2 - 4-тапсырма. Берілген тапсырмаларды орындаңдар. А) «Жолдама жайында» бөліміне...
1 - 8. Какими веществами загрязнены почвы, прилегающие к городам?...
1 - 9. Установіть відповідність між назвою регіону та його економічною спеціалізацією...
2 - 2. В чём смысл советов отца? 4. Озаглавьте каждую часть рассказа. Выпишите из...
2 - 7 сынып 119 бет 6 тапсырма...
1 - Характеристика героев по плану (Студент, профессорская дочка, Соловей) Примерный...
1 - 371. Прочитай текст-рассуждение. Найди в нём части рассуждения. Согласен(на)...
1 - быстреей Автордың спортқа қатысты ойларымен келісесің бе? Нелікте Спортпен шұғылданатын...
1
общее решение
частное решение
При х = 4
ответ: - 194