Тело движется прямолинейно по закону s=s(t), где s – путь, измеряемый в метрах, t – время, измеряемое в секундах. Найдите скорость и ускорение движения тела через две секунды после начала движения.
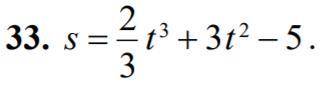
Другие вопросы по теме Математика
Популярные вопросы
- Английский язык кто знает ответы?...
1 - Визначте можливу інтенсивність пігментації шкіри дітей від шлюбу...
3 - Среди чисел: 4; – 3; 7; – 8 ; 4,5; 3; – 4,5 ; 6; – 5...
1 - Вывод о морфологических особенностях однодольных и двудольных...
2 - Сделайте тест по произведению «климко» Нужно буквы соединить...
2 - 4. Объем спальных комнат дома равен 1100 кубических метров....
2 - тапсырма Мәтіннен жалпы есімдерді теріп жазыныз 4 - тапсырма...
2 - Мальчик Паша исследовал зависимость силы тока, проходящего через...
2 - Жазылым. 2-тапсырма 40 бет. Мәтін бойынша грамматикалық тапсырма....
2 - Мәтін:Отбасы – Отанымыздың ошағыҚазақ отбасында баланың ерте...
3
1) Сначала найдем скорость. Скорость - это изменение пути по отношению к изменению времени. Она определяется как производная от функции пути по времени s(t).
Для нашего случая, у нас есть функция пути s(t), которая задана графически на рисунке. Чтобы найти скорость, необходимо найти тангенс угла наклона касательной к графику функции s(t) в точке t=2 секунды.
На рисунке, мы видим, что график функции s(t) является прямой линией, а значит, угол наклона будет одинаковым на любом отрезке этой прямой.
Таким образом, мы можем найти скорость, найдя тангенс угла наклона графика через две секунды после начала движения.
2) Теперь найдем ускорение. Ускорение - это изменение скорости по отношению к изменению времени. Ускорение определяется как производная от скорости по времени.
Для нашего случая, мы должны найти тангенс угла наклона касательной к графику функции скорости в точке t=2 секунды.
Для этого, сначала найдем скорость через две секунды после начала движения, используя процедуру, описанную в предыдущем пункте. Затем найдем график скорости v(t) в зависимости от времени. После этого, найдем угол наклона в точке t=2 секунды, который будет соответствовать ускорению.
Итак, в качестве ответа:
- Чтобы найти скорость движения тела через две секунды после начала движения, необходимо найти тангенс угла наклона графика функции пути s(t) в точке t=2 секунды.
- Чтобы найти ускорение движения тела через две секунды после начала движения, необходимо найти тангенс угла наклона графика функции скорости v(t) в точке t=2 секунды.
Для точного решения задачи, требуется предоставить конкретные значения функции пути s(t) и функции скорости v(t), чтобы определить точные значения скорости и ускорения через две секунды.