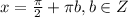Т3) Сколько корней имеет уравнение |cosx| + корень(sin2x) =0 на отрезке [0; 2пи] Заранее большое
![Т3) Сколько корней имеет уравнение |cosx| + корень(sin2x) =0 на отрезке [0; 2пи] Заранее большое](/tpl/images/3779/5884/461ca.jpg)
Другие вопросы по теме Математика
Популярные вопросы
- Мини-проект на тему где мы теряем воду?...
2 - 4.как доказать,что звуковая волна вляется продольной...
3 - Написать не большой рассказ по картинке как я однажды маме 10-15 предложений....
2 - Сочинение рассуждение на тему хлестаков и городничий. в чем их сходства и...
3 - Морфемный разбор слова смотришь, вырвалась. и морфологический разбор слов...
3 - При каком правителе появилась первая ярмарка...
3 - Устарика 7 сыновей, у каждого из них 7 сыновей, а у каждого внука старика...
1 - Период колебаний в волне радиоприемника 60 мкс. чему равна длина волны?...
2 - Особенности селекции 1.растений 2.животных 3. микроорганизмов вот например...
2 - Художественные образы герое из барышни крестьянки зарание...
2
Можно решить двумя Рассмотрим первый:
Исходя из этого понимаем, что выражение равно нулю только в том случае, если оба неотрицательных слагаемых равны нулю:
ответ: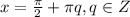
Второй
Данное уравнение равносильно следующей системе:
Так как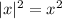 , то:
, то:
Модуль - это число неотрицательное. А это значит, что неравенство системы имеет смысл только тогда, когда cos(x) = 0:
Первое уравнение системы, очевидно, имеет решение cos(x) = 0. ответ получаем тот же.
ответ: