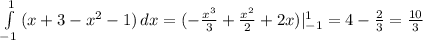Свышей в прямоугольник с вершинами к (-2,0), l (-2,5), м (1,5), n (1,0) брошена точка. какова вероятность того, что ее координаты(x,y) будут удовлетворять неравенству (x2+1)< =y< = (x+3)?
Другие вопросы по теме Математика
Популярные вопросы
- план до текста про золоте зернятко істини...
1 - Стр 117 4 тапсырма составить предложение и словосочетания...
3 - Якщо периметр основи правильної чотирикутної піраміди дорівнює 24...
2 - После перегонки нефти получают 30% газа. Сколько газа получат из...
2 - (-8;0), (-8; 7), (-9;9), (-8;9), (-7; 7), (1; 7), (4; 10), (4; 9),...
3 - Господар насипав пшеницю в мішки: у перший і другий по 40 кг, у третій...
3 - : a ⋅ c + b ⋅ c a ⋅ c – b ⋅ c a : c – b : c...
2 - Руда содержит 6% меди . Сколько необходимо взять руды, чтобы получить...
3 - Один із кутів, утворених при перетині двох паралельних прямих січною,...
1 - -13,5+(-7,9+4 1/5) как решить...
2
S(прямоугольника) = 3*5 = 15
S1(части) =