Сумма ряда
∑ 2^n/factorial(n + 3) или 2^n/(n + 3)!
n=1
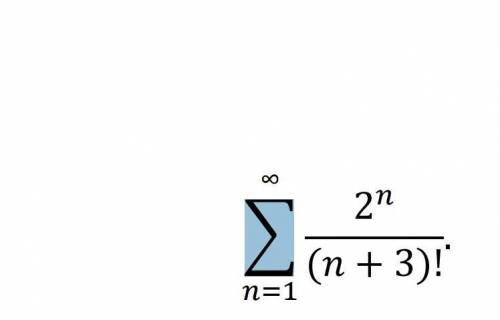
Другие вопросы по теме Математика
Популярные вопросы
- Рассчитай размеры элементов шипового соединения и запиши числа в пропуски...
2 - с заданием, очень надо! Вариантов ответа может быть сколько угодно....
3 - Лабораторная работа Тема. Определение возраста дерева по спилу стебля....
1 - Задание по алгебре 8 класс...
2 - с 211 номером, знаю косо сфотографировано, но все же...
3 - Водитель автобазы Медведев представил для оплаты лист нетрудо , в котором...
3 - 2.1. Сколько раз напечатается словосочетание «Итерация цикла» в результате...
3 - Упражнение 394. Перепишите, расставляя пропуішенные зна- ки препинания....
3 - ОЧЕНЬ НАДО составьте свой алгоритм приведения дробей к общему знаменателю...
2 - ответить на вопросы 1) Может ли быть массовая культура высокодуховной?...
3
Пошаговое объяснение: