(Строить график не надо,если можно)

Другие вопросы по теме Математика
Популярные вопросы
- 1. Розкрийте зміст історичних подій, уміщених на шкалі часу. Поясніть, як кожна...
2 - сор по каз яз 5класс 4 четверть...
2 - Нвйти тропы в стихе Ты помнишь, Алеша, дороги Смоленщины...
3 - Берілген ақпараттардың ішінен дұрыс/бұрыс тұжырымды анықтаңыз. Қазақ халқы...
1 - 1. На координатной плоскости отметьте точки А(14), B(-3;0), C(1; 6). ДС1;-5),...
3 - Осы тексттен жинакы матин керек ...
3 - Прочитайте два текста и выполните задание. Текст А. Отрывок из статьиАрхеологи...
2 - Можете один ответ написать хоть одиношеньку...
2 - 1. [ ] Найдите допустимые значения переменной в выражении X-0.56-3x 2. [ ]...
2 - Приведите пример, какие металлы и почему могут вытеснять водород из воды....
1
Пошаговое объяснение:
формула для оси симметрии х = - b/2a
расстояние между точками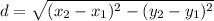
поскольку у нас точки пересечения с осью ОХ, они имеют координаты (х;0) и формула будет иметь вид d = х₂ - х₁
a) y=x² -4x +3
ось симметрии x = - (-4/2) = 2 x=2
точки пересечения с осью ОХ
x² -4x +3=0 ⇒ х₁= 1; х₂=3
точки (1;0) и (3;0)
расстояние между точками d = 3 - 1 = 2
b) y=x² + 2x -8
ось симметрии x = - (2/2) = 2 x= -1
точки пересечения с осью ОХ
x² + 2x -8=0 ⇒ х₁= -4; х₂=2
точки (-4;0) и (2;0)
расстояние между точками d = 2 - (-4) = 6
c) y=x² -4x -5
ось симметрии x = - (-4/2) = 2 x=2
точки пересечения с осью ОХ
x² -4x -5 =0 ⇒ х₁= -1; х₂= 5
точки (-1;0) и (5;0)
расстояние между точками d = 5 - (-1) = 6
d) y= -2x² + 4x + 6
ось симметрии x = - (4/4) = 1 x=1
точки пересечения с осью ОХ
x² -4x -5 =0 ⇒ х₁= -3; х₂= 3
точки (-1;0) и (3;0)
расстояние между точками d = 3 - (-1) = 4