Стрелок при каждом выстреле независимо от предыдущих попыток поражает цель с вероятностью 1/3. сделано 10 выстрелов. найдите вероятность того, что стрелок попал не менее двух раз, если известно, что хотя бы раз он попал

Ответы

геймер40 10.10.2020 06:20

Вероятность промаха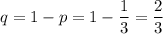 $q=1-p=1-\dfrac{1}{3}=\dfrac{2}{3}$

Пусть событие А - стрелок попал не менее двух раз, а событие В - попал хотя бы раз.

Вероятность того, что стрелок ни разу не попадет в мишень равна

$p_1=q^{10}=\dfrac{2^{10}}{3^{10}}$

Вероятность того, что стрелок попадет только один раз, равна

$p_2=C^1_{10}pq^{9}=\dfrac{10}{3}\cdot \dfrac{2^9}{3^9}$

Тогда вероятность того, что стрелок попадет не менее двух раз, равна

$P(A)=1-\Big(p_1+p_2\Big)=1-\Big(\dfrac{10}{3}\cdot\dfrac{2^9}{3^9}+\dfrac{2^{10}}{3^{10}}\Big)$

Вероятность того, что стрелок попадет хотя бы раз, равна

$P(B)=1-p_1=1-\dfrac{2^{10}}{3^{10}}$

Тогда по формуле Байеса, искомая вероятность:

$P(A|B)=\dfrac{P(B|A)*P(A)}{P(B)}=\dfrac{\left(1-\Big(\dfrac{10}{3}\cdot\dfrac{2^9}{3^9}+\dfrac{2^{10}}{3^{10}}\Big)\right)\cdot 1}{1-\dfrac{2^{10}}{3^{10}}}\approx0.912$

ответ: 0,912.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика

onealoner13 07.12.2021 15:00

УСЛОВИЯ ЗАДАЧИ И РАЗРЕШЕНИЕ ЗАДАЧИ.И И РАЗВЯЗАТЬ РИВНЯННЯ. МОЖНО ФОТКУ ПРИКРЕПИТЬ КАК РЕШАТЬ И УСЛОВИЯ МАТЕМАТИКА ШЕСТОЙ КЛАСС ДРОБИ...

niklysov2015 07.12.2021 14:59

Маса 40 м3повітря дорівнює 52 кг. Яка маса повітря в кімнаті, довжина якої 6м, ширина 4,5 м , а висота - 3 м?...

kseniya7117 07.12.2021 14:58

Построить изображение цилиндра вписанного в треугольную пирамиду. (Построение необходимо начать с построения цилиндра и около него описать правильную треугольную пирамиду). Нужен...

asca82 07.12.2021 14:58

16×7-75 -45+14×9 (31-12)×(32-62) !!♡♡♡...

BOILHbIU 07.12.2021 14:58

Ширина прямоугольника d м, длина в 8 раз больше, разность длины и ширины равна 14 м. Найдите его площадь....

hotnikita412 07.12.2021 14:58

Отметь отношения, из которых можно составить верную пропорцию: 6:4 0,5:4 3/4:0,5...

matveiruzkovjoping56 07.12.2021 14:58

В клетках квадрата 7×7 записаны неотрицательные числа так, что сумма всех чисел в любых двух соседних столбцах не меньше 16, а сумма всех чисел в любых двух соседних строках не больше...

R010KMB 07.12.2021 14:57

Шестикласники на літніх канікулах збирали різнотрав я. Збір трав складався з м яти, валер яни і ромашки у відношенні 5:3:2. Висушені трави діти пофасували в пакетики по 150 г кожен....

Титова2017 07.12.2021 14:57

6 в 3 степени вычесть 2 x 4 в 3 степени вычесть 1 в 3 степени...

Bigrash 07.12.2021 14:57

529, Найдите значения выражений: 1) 2) 317 11 : 3 +1 20 5 15 за 1 7 3 3) 4 : 1 ; 7 4. 4) 1 + 10 5 5 5 10 :1 8 1 5) 3: 1:15 6) 19 1 1 2 + 5 3...

Популярные вопросы