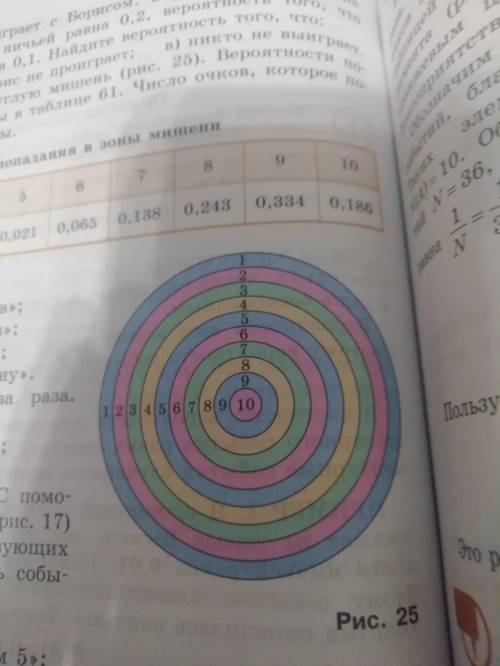
Стрелок один раз стреляет в круглую мишень. При этом вероятности попадания в зоны мишени представлены в таблице: Найдите вероятность события:
А)стрелок выбил меньше 5 очков
Б)стрелок выбил больше 7 очков
В)стрелок попал в желтую зону мишени
Г)стрелок попал в зеленую зону мишени
Д)стрелок не попал в голубую зону мишени
Е)стрелок попал в красную зону и при этом выбил больше 3 очков
Другие вопросы по теме Математика
Популярные вопросы
- Мне нужно! 10 вопросов по теме эпоха петра 1...
1 - Напишите письмо другу и выразите в нём по-какому либо поводу(за интересную...
2 - Вкаком из ответов правильно указана последовательность событий на...
1 - Из 75 одинаковых кубиков выложили прямоугольный параллелепипед высотой...
1 - Каждый из 20 учеников 9-ого класса записались хотя бы на один из трёх...
3 - Верно ли высказывание: (438*620-56 952): 526...
3 - Работа выхода электрона для никеля a = 4,84 эв. найти длину волны...
3 - Какие при позволяют людям использовать силу текучести воды?...
3 - Составьте схему предложения: все вокруг осветилось таинственным светом:...
3 - На уроке природоведения.дайте определения следующих понятий.обьясните...
3
Перед решением задачи нам необходимо разобраться с формулой вероятности. Вероятность события вычисляется как отношение количества благоприятных исходов к общему числу исходов.
Дано, что стрелок стреляет один раз в мишень, представленную на рисунке. Вероятности попадания в разные зоны мишени представлены в таблице. Давайте вычислим вероятность каждого заданного события.
А) Вероятность того, что стрелок выбил меньше 5 очков. Для этого нужно сложить вероятности попадания в зеленую, синюю и желтую зоны мишени.
P(меньше 5 очков) = P(зеленая) + P(синяя) + P(желтая) = 0.2 + 0.3 + 0.15 = 0.65
Ответ: Вероятность того, что стрелок выбил меньше 5 очков, равна 0.65.
Б) Вероятность того, что стрелок выбил больше 7 очков. Для этого нужно сложить вероятности попадания в красную, розовую и фиолетовую зоны мишени.
P(больше 7 очков) = P(красная) + P(розовая) + P(фиолетовая) = 0.05 + 0.1 + 0.15 = 0.3
Ответ: Вероятность того, что стрелок выбил больше 7 очков, равна 0.3.
В) Вероятность того, что стрелок попал в желтую зону мишени.
P(желтая зона) = 0.15
Ответ: Вероятность того, что стрелок попал в желтую зону мишени, равна 0.15.
Г) Вероятность того, что стрелок попал в зеленую зону мишени.
P(зеленая зона) = 0.2
Ответ: Вероятность того, что стрелок попал в зеленую зону мишени, равна 0.2.
Д) Вероятность того, что стрелок не попал в голубую зону мишени. Для этого нужно вычесть вероятность попадания в голубую зону мишени из единицы (так как сумма всех вероятностей равна 1).
P(не попал в голубую зону) = 1 - P(голубая) = 1 - 0.1 = 0.9
Ответ: Вероятность того, что стрелок не попал в голубую зону мишени, равна 0.9.
E) Вероятность того, что стрелок попал в красную зону и при этом выбил больше 3 очков. Для этого нужно умножить вероятность попадания в красную зону мишени на вероятность выбить больше 3 очков, так как эти события независимы.
P(красная и больше 3 очков) = P(красная) * P(больше 3 очков) = 0.05 * (0.1 + 0.15 + 0.05) = 0.05 * 0.3 = 0.015
Ответ: Вероятность того, что стрелок попал в красную зону и при этом выбил больше 3 очков, равна 0.015.
Надеюсь, ответы были понятны и я помог вам разобраться с этой задачей! Если у вас остались еще вопросы, не стесняйтесь задавать.