Столкнулся с непреодолимыми сложностями в решении этих вопросов в тесте: 15. Отношение "'быть старше': 'X старше Y'" является ?
- Рефлексивным
- Симметричным
- Транзитивным
- Антисимметричным
16. Количество нулевых значений таблицы истинности формулы: XYZ or (not X)YZ or X(not Y)(not Z), составляет ?
- 0
- 5
- 3
17. Отношение |X - Y| <= 1, заданное на множестве действительных чисел, являеться отношением ?
- толерантности
- поряжка
- эквивалетности
18. Задачи X, определяемое уравнением B = not(X or A) or not(X or not(A))
- B = not B
- X = B
- X = B/A
19. Отношения "X - победитель Y" является ?
- Антирефлексивный
- Симметричным
- Транзитивным
- Антисимметричным
20. Решите уровнение X and not((not X)Y), варианты ответов ?
- пустое множество
- Y
- X
- X or Y
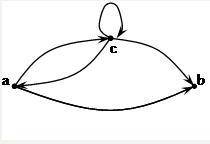
21. Матрица смежности для грфа <см. файл 2> имеед вид ?
- [0 0 1, 1 0 1, 1 0 1]
- [0 1 1, 0 0 0, 1 1 0]
- [0 1 1, 0 0 0, 1 1 1]
22. Каким подмножеством некоторого множества, явлеяется пустое множество ?
- собственное
- несобственное
- никакое
- не всегда является
23. Высказывание "Прозиведение целых чисел A и B не делиться на 2, в том и тольков том случаи, если A или B нечётное", в символической форме имеет вид ?
- (not C) <-> (not A) or (not B)
- (not C) <-> (not A) or (not B)
- A and B -> C
- A and B or C
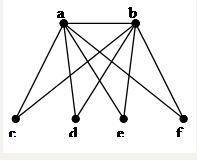
24. Хроматическое число графа равно <см. файл 3>
- 6
- 3
- 2
- 1
25. Если заданы два нечётких множества А{1|x1+0.3|x2+0.1|x3} и B{0.7|x1+0|x2+0.5|x3} то результат операции дополнения равен ?
- {0.7|x1+0|x2+0.5|x3}
- {1|x1+0.3|x2+0.1|x3}
- {0.3|x2+1|x2+0.5|x3}
- пустое множество
26. Если заданы два нечётких отношения A{1, 0.1, 0.2, 0.3} и B{0, 0.5, 0.6, 0.7}, то результат операции пересечения равен ?
- {1, 0.3, 0.5, 0.6}
- {1, 0.3, 0.1, 0.2}
- {0, 0.5, 0.6, 0.7}
- {0, 0.1, 0.2, 0.7}
27. Решите уровнение x and (x or y) =
- x^2 or xy
- x
- x or y
- пустое множество
28. Если заданы два нечётких отношние A{1, 0.1, 0.2, 0.3} и B{0, 0.5, 0.6, 0.7}, то результат операции объеденения равен ?
- {1, 0.3, 0.5, 0.6}
- {1, 0.2, 0.3, 0.5}
- {0, 0.5, 0.6, 0.7}
- {0, 0.1, 0.2, 0.7}
29. Если отношение A на множестве M рефлексивно, симметрично и транзитивно, то разбить множество М на непересекающиеся классы ?
- Можно
- Нельзя
- Можно, но не всегда
- Можно только в том случае, если А-отношение порядка
Ответы
Показать ответы (3)
Другие вопросы по теме Математика
Популярные вопросы
- :вычислите обьем шара и площадь его поверхности , если радиус шара равен...
3 - Впиши буквы в окончания имён существительных используя удобный для тебя...
3 - Нужно сделать памятку гражданину россии на тему: как сохранить растения...
1 - Вмагнитном поле с индукцией 2,5 тл находится проводник длиной 40 см рассположенный...
3 - Из какого числа меньше 28 можно отнять 3 раза по 9...
1 - Через два часа было только одно желание - выпить кружку горячего чая с...
2 - Как вы думаете, что самое главное в человеке? без чего бы человек не выглядил...
3 - Iam lady! -say the people. what do you like ladys? -say the bisnesmen....
3 - Как разделить 56 разделить на 2 в столбик...
3 - Перевод : она сказала, что идет дождь и нам лучше остаться дома ....
2