Срисунком в гранях двугранного угла проведены прямые а и b, параллельные его ребру, на расстоянии 10 см и 6см от него соответственно. найти величину этого двугранного угла, если расстояние между прямыми a и b равно 14см. 3)
равносторонний треугольник авс лежит в одной из граней двугранного угла, а сторона ав принадлежит его ребру. найти величину двугранного угла, если расстояние от вершины с треугольника до другой грани равно 2см, а сторона
треугольника 8корней из 3 деленное а 3 5) равносторонний треугольник аве и квадрат авсд лежат в гранях двугранного угла с ребром ав. найти величину двугранного угла если ав=4корней из 2см, ед=4см

1) Получаем треугольник AOB (см.рис1), стороны которого нам известны (AO=10 см, BO = 6 см, AB = 14 см). Из этого треугольника по теореме косинусов:

.

2) (см.рис2) Угол CDO - прямой, т.к. CD - расстояние от вершины С до грани угла (перпендикуляр). Значит, треугольник COD - прямоугольный, CO - гипотенуза. В то же время CO - высота равностороннего треугольника ABC. 

Из треугольника COD по определению синуса, синус угла COD равен отношению противолежащего катета CD к гипотенузе CO sinO= 2/4 = 1/2. То есть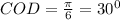 

3) (см.рис3) В треугольнике EOF сторона EO - это высота равностороннего трегольника ABE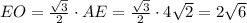 

Сторона OF равна стороне квадрата, DF равна половине стороны квадрата (OF - средняя линия ABCD), сторону EF найдём из прямоугольного треугольника EFD (EF перпендикуляр к CD => EFD - прямоугольный, ED - гипотенуза): .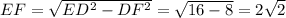

Тогда из треугольника EOF по тереме косинусов: