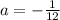Срешение, )) найти наибольшее и наименьшее среди значений параметра а, при которых неравенство 3а+1/4-ах+а^2х^2< =(больше либо равно) 0 выполняется при всех х из отрезка [-1; 0].
Другие вопросы по теме Математика
Популярные вопросы
- ерунду всякую непишем С интернета непереписоваем ...
2 - Вариант 2 1. Среди учащихся б классов был проведен опрос: сколько времени вы...
1 - Если d - pасстояние между центром окружности и прямой, а r- радиус окружности...
2 - Берилген матинди тусмнип окы орман ишинде ток ток еткен дыбыс естидим жан жагыма...
3 - определите модуль силы Лоренца действующей на частицу заряд которой равен 5м...
3 - Дайте определение:1. Авторское право - это......
3 - (-:пословицы к рассказу Михаила Зощенко Находка ...
2 - 1). Что больше и во сколько раз : 8!∙6 или 7!∙12 ? 2). Вычислить значение выражения...
3 - Человек, рост которого составляет 167 см, стоит под фонарём. Его тень при этом...
3 - 2). Опираясь на карту, ответьте на вопросы: 1. Куда была направлена первая...
3
Рассмотрим функцию
1. a = 0. График - прямая линия.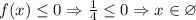 . Значение параметра не подходит.
. Значение параметра не подходит.
2. a ≠ 0. График - парабола, ветви направлены вверх,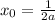 .
.
Если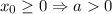 , то
, то ![f(-1)\leq 0 \Rightarrow a^2+4a+\frac{1}{4}\leq 0 \Rightarrow a\in[\frac{-4-\sqrt{15}}{2}; \frac{-4+\sqrt{15}}{2}]\Rightarrow a\in\varnothing](/tpl/images/0946/0037/5687c.png)
Если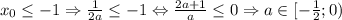 , то
, то ![f(0)\leq 0 \Rightarrow 3a+\frac{1}{4}\leq0 \Leftrightarrow a \leq -\frac{1}{12} \Rightarrow a\in[-\frac{1}{2}; -\frac{1}{12}]](/tpl/images/0946/0037/a2f5d.png)
Если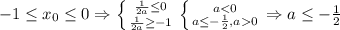 , то
, то ![\left \{ {{f(0)\leq0} \atop {f(-1)\leq0}} \right. \left \{ {{a\in(-\infty; -\frac{1}{12}]} \atop {a\in[\frac{-4-\sqrt{15}}{2}; \frac{-4+\sqrt{15}}{2}]}} \right. \Rightarrow a\in[\frac{-4-\sqrt{15}}{2}; -\frac{1}{12}] \Rightarrow a\in[\frac{-4-\sqrt{15}}{2}; -\frac{1}{2}]](/tpl/images/0946/0037/e650b.png)
Тогда![a\in[\frac{-4-\sqrt{15}}{2}; -\frac{1}{12}]](/tpl/images/0946/0037/f5c9a.png)
ответ: наименьшее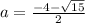 , наибольшее
, наибольшее