Спростіть вираз cos²a/1-sin a
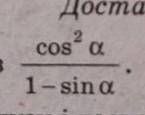
Другие вопросы по теме Математика
Популярные вопросы
- Написать сочинение по язык это очки,без которых нам не разглядеть окружающий...
3 - Сочинение на лингвистическую тему: л.в.успенский грамматика не только...
2 - За блокнот федя заплатил 4/15 имеющихся у него денег, а слава за альбом...
2 - Употреби имена дмитрий, дима в предложениях.какими членами предложениях...
1 - Определи животное по описанию запиши ответ этот хищник обладает незаурядным...
3 - Укажите все общие делители числа 24 и18 найди нод (24; 18)...
2 - Составить кроссворд по теме средства массовой информации ....
2 - Масса ядра равна 8 кг. расстояние от центра ядра до плечевой кости равно...
3 - Поставь данные имена существительныепоставь данные имена существительные...
2 - Почему в представленных ситуациях целесообразно прибегать к моделированию?...
1
1+sin(a)
Пошаговое объяснение:
Запишем основное тригонометрическое тождество
cos²a+sin²a=1
Вычтем из обеих частей sin²a,тогда
cos²a=1-sin²a, пусть синус альфа это какая-то переменная b,тогда выражение будет иметь вид: cos²a=1-b², 1 в любой степени это 1, в т.ч. и во второй, тогда cos²a=1²-b²
1²-b²=(1-b)(1+b). Вернем обратную замену.
cos²a=(1-sina)(1+sina), тогда числитель и знаменатель можно сократить на 1-sina, а значит ответ 1+sina