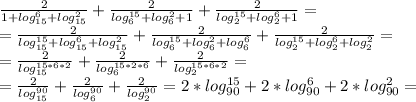Спервым примером №2.53, у меня совсем не получается сделать что-то со знаменателем, я уже и на дискриминант выходила, но все не то. 30 ‼️‼️‼️✨
Другие вопросы по теме Математика
Популярные вопросы
- Найдите слово которое в современном языке имеет иное грамматическое...
2 - Солнце воздух и вода растпространить! нужно солнце воздух и...
1 - Укажите предложение в котором слово язык выступает в роли несогласованного...
1 - Найдите с пропорции 5% от числа 60...
1 - Из вертолета, движущегося горизонтально со скоростью 40 м/с,...
3 - Камень брошен вертикально вверх со скоростью 30 м с. масса камня...
2 - Какая ускоряющая разность потенциала требуется для того чтобы,...
2 - На каком расстоянии друг от друга зарядом 1 микрокулон и 10...
2 - 7,8a+2,3a-5a при а=6 тема: обратно пропарциональные величины...
2 - Вставить в приложение имена собственные в республике казахстан...
2
1) 1
2) 2
Пошаговое объяснение:
1)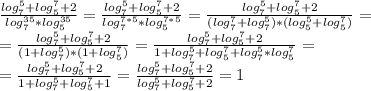
2)