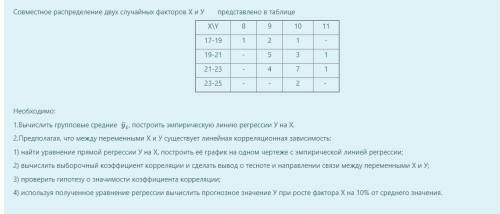
Совместное распределение двух случайных факторов X и У представлено в таблице: (Задания на скриншоте)
Другие вопросы по теме Математика
Популярные вопросы
- Почему до сих пор существуют подсолнечники-ответ на легенду...
1 - (разделить текст на предложения) у люси широковой есть пёс форд а ляле жижиной...
3 - Сравнить повесть м.горького детство и л.н....
2 - Папа принёс с базара арбуз.за ужином папа съел 1/4 часть арбуза,мама съела 1/5...
2 - Коэффициент полезного действия некоторой тепловой машины составляет 60% от кпд...
2 - Найдите 4 числа, первые 3 из которых состовляют убывающую арефметическую прогрессию,...
1 - Нужно придумать загадку про фею на языке....
2 - Вцилиндрическом сосуде уровень жидкости достигает 125 см. на какой высоте будет...
2 - распространения семян: репейника, акации, шиповника. по возможности при каждого...
1 - Чи мрієш ти побувати на екскурсії або вирушити в похід? що саме хочеш там побачити?...
1
Здесь представлена совместная таблица распределения двух случайных факторов X и Y. В этой таблице указаны все возможные значения X и Y, а также вероятности их сочетаний.
Давайте определим, что такое совместное распределение. Совместное распределение двух случайных факторов X и Y описывает вероятности их сочетаний. В данном случае X принимает значения 1, 2 и 3, а Y принимает значения 1, 2 и 3.
Для ответа на вопрос, давайте сначала найдем вероятности для каждого из значений X и Y.
Для этого вычислим сумму вероятностей в каждой строке и в каждом столбце таблицы. Например, для значения X=1 сумма вероятностей в строке будет равна 0.2 + 0.1 + 0.05 = 0.35.
Теперь давайте найдем вероятность для каждой пары значений X и Y. Например, для X=1 и Y=1, вероятность будет равна 0.2.
Теперь мы можем ответить на вопрос.
Для нахождения математического ожидания случайной величины X, мы будем использовать формулу:
E(X) = сумма (значение X * вероятность(X))
В нашем случае, сумма будет состоять из трех слагаемых:
E(X) = (1 * 0.35) + (2 * 0.25) + (3 * 0.4) = 0.35 + 0.5 + 1.2 = 2.05
Таким образом, математическое ожидание случайной величины X равно 2.05.
Аналогично, мы можем найти математическое ожидание случайной величины Y, используя формулу:
E(Y) = сумма (значение Y * вероятность(Y))
В нашем случае, сумма будет состоять из трех слагаемых:
E(Y) = (1 * 0.25) + (2 * 0.3) + (3 * 0.45) = 0.25 + 0.6 + 1.35 = 2.2
Таким образом, математическое ожидание случайной величины Y равно 2.2.
Надеюсь, этот ответ понятен для вас. Если у вас возникнут еще какие-либо вопросы, пожалуйста, не стесняйтесь задавать их.
ответ не понел вапше
Пошаговое объяснение: