Составте уравнение плоскости проходящей через точку А(1,-2,1) перпендикулярно прямой 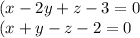
Другие вопросы по теме Математика
Популярные вопросы
- Сколько граммов меди потребуется для реакции с 50 мл раствора разбавленной азотной...
3 - От одного металлов, который именованный на низе, другой на природе на чистом целное...
1 - Какие элементы iiв группы реагируют с соляной кислотой и разбавленной серной кислотой?...
3 - Сочинить фантастическую сказку о мальчике кот живет на таинственном острове один...
3 - Площадь квадрата равна 64 см2. чему будет равен его периметр?...
3 - Подберите синонимы к словам: необычность- нелепица- несчастье- заранее ))...
1 - Найдите экстремумы функции f(x) = x^3*lnx...
1 - Втреугольнике авс угол с раен 45градусов, ad-бессиктриса угла а, угол adb равен...
2 - По теории вероятности! команда премьер-лиги, встречаясь в матче на кубок россии...
3 - Зависимость объема спроса q (единиц в месяц) на продукцию предприятия-монополиста...
3
Направляющий вектор прямой, образованной пересечением двух плоскостей А1x+B1y+C1z+D1=0 и A 2 x+B2y+C2z+D2=0, будет перпендикулярен нормальным векторам
→n1=(A1, B1, C1) и →n2=(A2, B2, C2 )
. То есть в качестве направляющего вектора мы может взять произведение векторов
→ n1=(A1, B1, C1) и →n2=(A2, B2, C2).
Нормальные векторы исходных плоскостей n1(1,-2,1) и n2(1,1,-1).
Находим их векторное произведение.
i j k| i j
1 -2 1| 1 -2
1 1 -1| 1 1 = 2i + 1j + 1k + 1j - 1i + 2k = 1i + 2j + 3k.
Нашли направляющий вектор прямой, по которой пересекаются исходные плоскости: n(1; 2; 3).
Этот вектор является нормальным вектором перпендикулярной плоскости.
Её уравнение: 1(x - 1) + 2(y + 2) + 3(z - 1) = 0.Раскроем скобки.
x - 1 + 2y + 4 + 3z - 3 = 0 или x + 2y + 3z = 0.
ответ: x + 2y + 3z = 0.