Составить уравнение касательной и уравнение нормали к
данной кривой в точке с абсциссой
X0
y=(x^5+1)/(x^4+1), x0=1
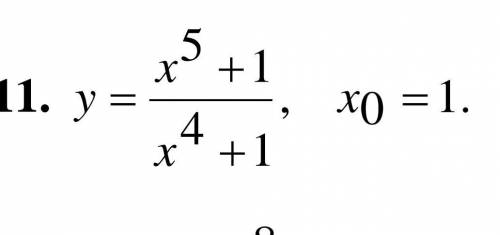
Другие вопросы по теме Математика
Популярные вопросы
- Было 7 яблок. Съели 4. Сколько осталось яблок?...
3 - Нужно по свежим новостям сделать. Номер 2!!...
2 - С ЕСТЕСТВОЗНАНИЕМ (чтобы увидеть откройте полностью)...
2 - Лёгкое задание слова с таблиц по вставлять....
2 - Визначте присудок і підмет у реченні Як тепло і добре хорошим...
3 - НУЖНО ПОДРОБНОЕ РЕШЕНИЕ С динамометра измерили вес медного бруска...
1 - Контрольная работа по химии...
2 - Чем характеризовалась экономическая жизнь в Римской империи в...
1 - Підкресліть граматичну основу .А лихо в друга – поспішай до нього...
1 - Сделать по основам грамматики английского языка: The Titanic (cross)...
1
касательная: y=x
нормаль: y=-x
Пошаговое объяснение:
y=(x⁵+1)/(x⁴+1); x(0)=1;
1. вычислим y(0):
y(0)=y при х=х(0).
y(0)=[(1⁵+1)]/[(1⁴+1)]=2/2=1;
y(0)=1;
2. возьмем производную:
y'=[(x⁵+1)/(x⁴+1)]';
y'=[(x⁵+1)*(x⁴+1)⁻¹]'=(x⁵+1)'(x⁴+1)⁻¹+[(x⁴+1)⁻¹]'(x⁵+1)=5x⁴(x⁴+1)⁻¹- 4x³(x⁴+1)⁻²*(x⁵+1)=
=5x⁴/(x⁴+1)-4x³*(x⁵+1)/(x⁴+1)²;
y'=[5x⁴(x⁴+1)-4x³(x⁵+1)]/[(x⁴+1)²]:
3. вычислим y'(0) т.е. при x=x(0):
y'(0)=[5*1⁴(1⁴+1)-4*1³(1⁵+1)]/[(1⁴+1)]=[5*2-4*2]/2=1.
4.
a) касательная:
y-y(0)=y'(0)(x-x(0)); x(0)=1; y(0)=1; y'(0)=1
y-1=1*(x-1);
y=x-1+1;
y=x
b) нормаль
y-y(0)=-1/y'(0)(x-x(0);
y-1=-1/1(x-1);
y=-x