Составь математическую модель по словесной: периметр прямоугольника равен 44 см, а площадь — 117 см2.
Найди длину и ширину прямоугольника.
Выбери подходящую математическую модель, обозначив
длину прямоугольника как p см, а
ширину — a см:
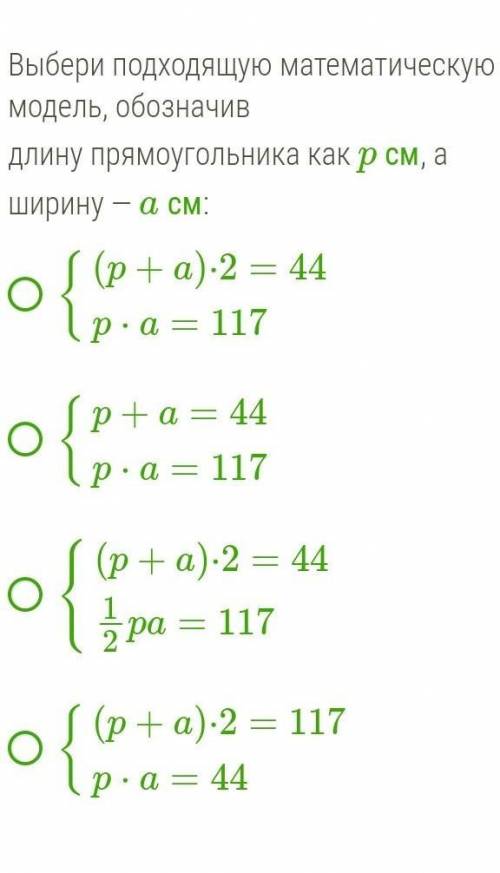
Другие вопросы по теме Математика
Популярные вопросы
- 100 ! ! из точки м проведён перпендикуляр мд,равный 6см,к плоскости...
1 - Что изобрели в средние века в японии...
1 - Нужно сочинение на тему тургенев муму не сильно большое....
2 - Чему равен угол, если два смежных с ним угла составляют в сумме...
1 - Опишите животных на : 3 любое животное)...
2 - Составить предложение с этим словом относиться с уважением к...
2 - Решить.выпиши выражения, значения которых делятся на 4. (72-64)×2...
2 - К! жизнь костылина в плену пересказ....
2 - Вмагазин 48 ящиков желтой и красной черешни. число ящиков с...
3 - Решение уравнений: а) -(7-3у)=8-8(2-у)...
2
Для решения данной задачи, воспользуемся формулами для периметра и площади прямоугольника.
Периметр прямоугольника равен сумме длины всех его сторон. В данном случае у нас есть две стороны прямоугольника: длина (p) и ширина (a). Поэтому, математическая модель для периметра прямоугольника будет следующей:
2p + 2a = 44.
Площадь прямоугольника вычисляется как произведение его длины и ширины. Также у нас есть информация о площади прямоугольника, которая равна 117 квадратным сантиметрам. Следовательно, математическая модель для площади прямоугольника будет следующей:
p * a = 117.
У нас есть два уравнения с двумя неизвестными (p и a), и мы можем решить их методом замены или методом сложения/вычитания.
Давайте воспользуемся методом сложения/вычитания для решения этой системы уравнений.
Уравнение 1: 2p + 2a = 44.
Уравнение 2: p * a = 117.
Умножим уравнение 1 на 2, чтобы избавиться от коэффициента 2 в первом уравнении:
4p + 4a = 88.
Затем вычтем это новое уравнение из уравнения 2:
(p * a) - (4p + 4a) = 117 - 88,
p * a - 4p - 4a = 29.
Теперь мы можем преобразовать это уравнение следующим образом:
p * a - 4p - 4a + 16 = 29 + 16,
(p - 4)(a - 4) = 45.
Теперь нам нужно найти два числа, которые в сумме дают 45 и при этом их произведение равно 45.
Разложим 45 на простые множители: 1 * 45, 3 * 15, 5 * 9.
Попробуем подставить эти значения в уравнение (p - 4)(a - 4) = 45 для определения длины и ширины прямоугольника:
- Если p - 4 = 1 и a - 4 = 45, то p = 5 и a = 49. Это не может быть ответом, так как получаются отрицательные значения сторон прямоугольника.
- Если p - 4 = 3 и a - 4 = 15, то p = 7 и a = 19. Это также не может быть ответом, так как получаются нецелые значения сторон прямоугольника.
- Если p - 4 = 5 и a - 4 = 9, то p = 9 и a = 13. Это может быть ответом, так как получаем целые положительные значения для сторон прямоугольника.
Итак, длина прямоугольника составляет 9 см, а ширина - 13 см.
Надеюсь, это решение будет понятным для вас! Если у вас возникнут еще вопросы, пожалуйста, не стесняйтесь задавать. Я всегда готов помочь!