Собака привязана к поводку длины 2, другой конец которого может свободно скользить по катетам ав и вс прямоугольного треугольника авс. известно, что ас=10 и угол вас=60градусов. какова длина части отрезка ас, до которой собака не может добраться? а) 2 б) 4 в) 6 г) 10 - 4 корня из 2 д) 6- 4корня из 3\3

д)

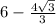
Пошаговое объяснение:

Известно, что гипотенуза АС прямоугольного треугольника АВС равна 10 и ∠ВАС=60°.

Определим длины катетов АВ и ВС:

AB=AC·cosn60°=10·1/2=5,

BC=AC·sins60°=10·√3/2=5√3.

Собака с поводком длиной 2 двигаясь по катетам АВ и ВС прямоугольного треугольника АВС может достичь (см. рисунок) все точки от А по N и от L по C.

Поэтому, чтобы определить длина части отрезка АС, то есть длину отрезка  NL, до которой собака не может добраться определим длину отрезка АN и LC.

Так как ∠MAN=∠BAC, ∠AMN=∠ABC=90°, ∠ANM=∠ACB, то

треугольники ΔAMN и ΔABC подобны. Тогда из-за подобия треугольников ΔAMN и ΔABC:

или AN=AC·MN/BC=10·2/(5√3)=4/√3=4√3/3.

Также ∠LCK=∠ACB, ∠LKC=∠ABC=90°, ∠CLK=∠CAB, то

треугольники ΔLKC и ΔABC подобны. Тогда из-за подобия треугольников ΔLKC и ΔABC:

или LC=AC·LK/AB=10·2/5=4.

Тогда длина части отрезка АС, до которой собака не может добраться

NL=AC-АN-LC=10-4√3/3-4=6-4√3/3.