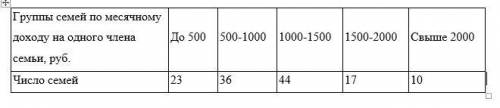
Случайным бесповторным проведено выборочное обсле¬дование семей района. Из 1300 семей обследовано 130, по которым определен душевой доход на одного члена семьи, представленный в виде интервального вариационного ряда. Распределение семей по величине месячного дохода на одного члена семьи: С доверительной вероятностью 0,95 определить границы, в кото¬рых будет находиться средний месячный доход на одного члена семьи по району, а также доля семей с доходами, менее 1000 руб. на одного члена семьи.

Для решения данной задачи нам потребуется найти доверительный интервал для среднего значения и долю семей с доходами менее 1000 руб. на одного члена семьи.

1. Найдем среднее значение и стандартное отклонение для выборки:
- Для этого построим таблицу, в которой укажем середину каждого интервала и сумму частот:
```
Интервал Частота Середина
(800-1000] 5 900
(1000-1200] 6 1100
(1200-1400] 18 1300
(1400-1600] 27 1500
(1600-1800] 30 1700
(1800-2000] 32 1900
(2000-2200] 12 2100
```
- Найдем среднее значение, умножив каждую середину на соответствующую частоту и поделив сумму всех таких произведений на сумму всех частот:
```
(5*900 + 6*1100 + 18*1300 + 27*1500 + 30*1700 + 32*1900 + 12*2100) / (5 + 6 + 18 + 27 + 30 + 32 + 12) = 1564.39
```
Таким образом, средний месячный доход на одного члена семьи по району составляет 1564.39 руб.

- Для нахождения стандартного отклонения, посчитаем сумму квадратов разностей между серединами интервалов и средним значением, умноженных на соответствующие частоты:
```
(5*(900 - 1564.39)^2 + 6*(1100 - 1564.39)^2 + 18*(1300 - 1564.39)^2 + 27*(1500 - 1564.39)^2 + 30*(1700 - 1564.39)^2 + 32*(1900 - 1564.39)^2 + 12*(2100 - 1564.39)^2) / (5 + 6 + 18 + 27 + 30 + 32 + 12) = 120441.84
```
Затем найдем стандартное отклонение, возведя в квадрат сумму квадратов и поделив на общую частоту, вычтя из полученного значения квадрат среднего значения и извлекши корень из полученного значения:
```
sqrt(120441.84 / (130 - 1)) = 167.86
```
Таким образом, стандартное отклонение равно 167.86.

2. Найдем доверительный интервал для среднего значения.
- Для этого воспользуемся формулой доверительного интервала для среднего значения с известным стандартным отклонением:
```
Доверительный интервал = Среднее значение +/- (Z * (Стандартное отклонение / sqrt(Объем выборки)))
```
Где Z - критическое значение для указанной доверительной вероятности. Для доверительной вероятности 0.95 значение Z равно 1.96.
Подставим известные значения в формулу:
```
Доверительный интервал = 1564.39 +/- (1.96 * (167.86 / sqrt(130)))
```
Вычисляем:
```
Доверительный интервал = 1564.39 +/- (1.96 * 14.67) = 1564.39 +/- 28.77
```
Таким образом, средний месячный доход на одного члена семьи по району будет находиться в интервале от 1535.62 до 1593.16 руб.

3. Найдем долю семей с доходами менее 1000 руб. на одного члена семьи.
- Для этого найдем сумму частот всех интервалов, в которых значения меньше 1000 и поделим на общую сумму частот:
```
(5 + 6) / 130 = 0.077
```
Таким образом, доля семей с доходами менее 1000 руб. на одного члена семьи составляет 0.077.

Итак, средний месячный доход на одного члена семьи по району будет находиться в интервале от 1535.62 до 1593.16 руб. Соответственно, доля семей с доходами менее 1000 руб. на одного члена семьи составляет 0.077.