Случайная величина ξ имеет нормальное распределение. Известно, что P(X < 0,44) = 0,1 а P(X ≥ 3,88) = 0,33. Найти плотность
распределения ξ и построить ее график.
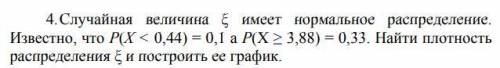
Другие вопросы по теме Математика
Популярные вопросы
- Описание розы на казаском языке 6класс...
3 - Два трактора вспахали поле за 6 часов работы по отдельности, первый...
2 - 10 вопросов к произведению черкашина кукла,,...
3 - 1. x квадрат+7x+6=0 2. x квадрат +x=56 3. 3х квадрат + 5х - 2 = 0...
1 - Какие 3-х значные числа можно составить из цифр: 0,2,4(числа могут...
3 - Отличия герды и снежной королевы подскажите...
3 - Составте два уравнения реакций , доказывающих , что оксид серы 6 обладает...
3 - Випишіть з підручника ії чи історії 3-5 речень із прислівниками вищого...
1 - Напишите небольшое сочинение про три псевдонимы антона павловича чехова...
2 - Синтаксический разбор показавшееся из-за туч солнце ярко осветило...
3
Мы знаем, что случайная величина ξ имеет нормальное распределение. Из этой информации мы можем сделать вывод о том, что плотность распределения ξ будет иметь форму колокола.
Исходя из данных задачи, нам известны две вероятности: P(X < 0,44) = 0,1 и P(X ≥ 3,88) = 0,33. Эти вероятности могут помочь нам определить параметры нормального распределения.
Вероятность P(X < 0,44) = 0,1 означает, что площадь под графиком функции плотности распределения от минус бесконечности до 0,44 равна 0,1. Аналогично, вероятность P(X ≥ 3,88) = 0,33 означает, что площадь под графиком функции плотности распределения от 3,88 до плюс бесконечности равна 0,33.
Теперь нам нужно найти параметры нормального распределения - математическое ожидание (μ) и стандартное отклонение (σ).
Для начала найдем μ. Мы знаем, что P(X < 0,44) = 0,1, поэтому можем использовать таблицы нормального распределения или специальные программы для вычисления z-значения (значение стандартной нормальной случайной величины) для данной вероятности. После нахождения z-значения, мы сможем использовать обратную функцию стандартного нормального распределения, чтобы найти соответствующее z-значение. Затем мы можем использовать формулу связи между x и z, чтобы найти μ.
Аналогично, для нахождения σ, мы можем использовать вероятность P(X ≥ 3,88) = 0,33. Найдя z-значение соответствующее этой вероятности, мы сможем использовать обратную функцию стандартного нормального распределения, чтобы найти σ.
После нахождения μ и σ, мы сможем построить график плотности распределения ξ. На этом графике ось x будет представлять значения случайной величины ξ, а на оси y будет обозначена плотность распределения, которая будет иметь форму колокола.
Итак, мы должны вычислить μ и σ с использованием данных вероятностей и построить график плотности распределения ξ.
Для проведения таких расчетов необходимы дополнительные данные о характеристиках нормального распределения, такие как среднее значение и стандартное отклонение. Без этих данных я не могу дать конкретный и подробный ответ на данный вопрос.