Сколько пар целых чисел (m, n) имеется удовлетворяющих равенство mn+n+14=(m-1)(m-1)

ответ: 8 пар.

Объяснение:

Раскрыв скобки, получаем:

Перенесем слагаемые с переменными влево, а свободный член — вправо:

Из обеих частей уравнения вычтем :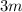

Разложим левую часть на множители методом группировки:

К обеим частям уравнения прибавим выражение :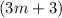

Вынесем общий множитель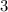 за скобки:

Вынесем :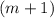

Так значения m и n целые (по нужному условию), значения выражений в скобках не могут быть дробными.

Произведение двух целых чисел равно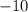 в восьми случаях:

1) ;

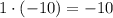2) ;

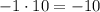3) ;

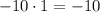4) ;

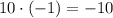5) ;

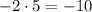6) ;

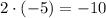7) ;

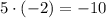8) .

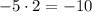Определим, какие будут значения m и n, если значения выражений в скобках равны множителям из каждого случая:

1)

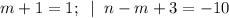
Получаем:

Значит, (m,n) = (0; -13).

Аналогично рассмотрим следующие случаи:

2)

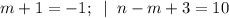
(m,n) = (-2; 5).

3)

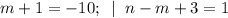
(m,n) = (-11; -13).

4)

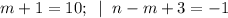
(m,n) = (9; 5).

5)

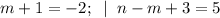
(m,n) = (-3; -1).

6)

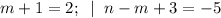
(m,n) = (1; -7).

7)

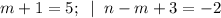
(m,n) = (4; -1).

8)

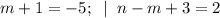
(m,n) = (-6; -7).

Выходит, 8 пар целых чисел (m, n) удовлетворяют данное равенство.