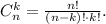Сколько комбинаций может быть при отборе из 16 человек (10 девушек и 6 мужчин) команды из 7 человек, при условии, что в состав 7 должны входить 2 девушки и 5 мужчин? Cколько комбинаций может быть при отборе из 20 человек (9 мужчин и 11) женщин) команды из 7 человек=2 женщины + 5 мужчин?
Другие вопросы по теме Математика
Популярные вопросы
- Представьте выражение в виде многочлена (-x+5)^2...
1 - Сторона квадрата дорівнює 30 см. чому дорівнює його площа, і що таке площа?...
2 - Из предложений 20—25 выпишите слово, в котором правописание суффикса определяется...
2 - Придумай предложение с каждым из синонимов интересный забавный занимательный...
3 - составьте предложения, в которых указанные ниже слова были бы в одном случае подлежащим,...
2 - Народ 1. что такое реконкиста? назовите сходства и различия между реконкистой и...
1 - Оцініть периметр квадрата зі стороною a см, якщо 1,2 a 1,8. ,...
1 - 3. запишите закон сохранения импульса для движения ракеты, предположив, что все...
2 - Обьяснить смысл поговорки: кто долго жуёт,тот долго живёт...
2 - Замените книжное слово «благоговейно» в предложении 22 стилистически нейтральным...
2
1) 270
2) 6930
Пошаговое объяснение:
По правилу умножения комбинаторики количество таких комбинаций равно произведению числа которыми можно выбрать девушек на число которыми можно выбрать мужчин.
Задача 1. Число для девушек и мужчин найдем по формуле сочетаний:
Считаем: n * m = 45 * 6 = 270
Задача 2. Число для девушек и мужчин найдем по формуле сочетаний:
Считаем: n * m = 55 * 126 = 6930
Для справки: пусть имеется n различных объектов, тогда число сочетаний из n объектов по k рассчитывается по формуле: