Сколькими нулями оканчивается произведение последовательных натуральных чисел от 1 до 50? 1 23**48 4950

Ответы

KindPioneer 05.08.2020 09:58

$1\cdot 2\cdot 3\cdot 4\cdot...\cdot48\cdot49\cdot 50=50!$

Подсчитаем сколько раз приходится число 2 в факториал 50

$[\frac{50}{2}]+[\frac{50}{2^2}]+[\frac{50}{2^3}]+[\frac{50}{2^4}]+[\frac{50}{2^5}]=25+12+6+3+1=47$

В разложении числа 50! двойка встречается ровно 47 раз.

Найдем теперь сколько раз приходится число 5 в факториал 50

$[\frac{50}{5}]+[\frac{50}{5^2}]=10+2=12$

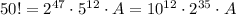Значит $50!=2^{47}\cdot 5^{12}\cdot A=10^{12}\cdot 2^{35}\cdot A$ , где А - некоторый множитель. Видим, что число оканчивается 12 нулями.

ответ: 12.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика

Srednov 24.09.2019 03:30

MadamHlebushek11 24.09.2019 03:30

1)4(х-2)= 16 2)2(3+2х)=4(3х)+26 3)-4(7-х)=х-16 4)3х+7=8х-3 по братски...

аркадий47 24.09.2019 03:30

{2х+3у=18 {5х-6у=-9 можете сделать в тетради...

carevruslan 24.09.2019 03:30

Diana2004250 24.09.2019 03:30

1. решите уравнение при а=-1/3; 2(0,3а-1)-2/5(3а-5)=...

karmazinakata67890 24.09.2019 03:30

Найдите значение вырожения (-4..55)): 3.2-1.2•(-0.6)...

Рома2043 24.09.2019 03:40

popdaniela820 24.09.2019 03:40

Хелп ми х -3,5)•(-1,5)=(2,3x-9)•0,5...

nikzyk 24.09.2019 03:40

Решите выражение : 5x-(x+2) при x= - 6...

228ANONIM1337 24.09.2019 03:40

Сколькими нулями оканчивается произведение последовательных натуральных чисел от 1 до 50? 1 *2*3**48 *49*50​