Сколькими можно выбрать две детали из ящика, содержащего 10 деталей?

Ответы

Kseniya1111111120 11.08.2020 01:50

Пошаговое объяснение:

Задачу решаем двумя

1. Пронумеруем детали с 1 по 10. Тогда выбор 2 деталей можем описывать следующим образом:

1) с 1-ой деталью на паре могут быть детали со 2 по

2) со 2-ой деталью на паре могут быть детали с 3 по так как пара с 1-ой деталью уже учли;

...

8) с 8-ой деталью на паре могут быть детали с 9 по так как пара с 1-ой по 7 уже учтены;

9) с 9-ой деталью на паре может быть 10-ая деталь так как пара с 1-ой по 8 уже учтены.

А для 10-ой детали все пары уже учтены. Тогда количество всего:

9+8+7+6+5+4+3+2+1=45.

2. Число сочетаний из N элементов по M с формулы комбинаторики:

$\displaystyle C^{M}_{N}=\dfrac{N!}{M! \cdot (N-M)!}$ , где факториал K!=1·2·3·...·(K–1)·K.

В нашем случае число равно числу сочетаний из 10 деталей по 2, то есть равно: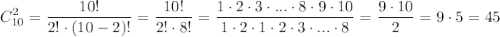 $\displaystyle C^{2}_{10}=\dfrac{10!}{2! \cdot (10-2)!}=\dfrac{10!}{2! \cdot 8!}=\dfrac{1 \cdot 2 \cdot 3 \cdot ... \cdot 8 \cdot 9 \cdot 10}{1 \cdot 2 \cdot 1 \cdot 2 \cdot 3 \cdot ... \cdot 8}=\dfrac{9 \cdot 10}{2}=9 \cdot 5 = 45$ .