Сколькими читатель может выбрать три книжки из пяти имеющихся?

Ответы

banana1106 12.07.2020 10:20

Пошаговое объяснение:

Для решения задачи надо найти сочетание из 5 элементов по 3.

Воспользуемся формулой

$C^{k} _{n} = \frac{n!}{k!(n-k)!}$

Тогда

$C^{3} _{5} =\frac{5!}{3! (5-3)!} =\frac{5!}{3!*2!} =\frac{3!*4*5}{3!*1*2} =10$

ПОКАЗАТЬ ОТВЕТЫ

niklassn 12.07.2020 10:20

Пошаговое объяснение:

Пусть из множество A берется сразу несколько элементов. В результате такого одновременного неупорядоченного выбора k элементов из множества A, состоящего из n элементов, получаются комбинации выбора), которые называются сочетаниями без повторений из n элементов по k (количество выбора).

Число сочетаний из n элементов по k обозначается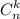 $\displaystyle C_{n}^{k}$ и равно:

$\displaystyle C_{n}^{k} =\frac{n!}{k! \cdot (n-k)!},$

где m!=1·2·3·...·(m-1)·m.

Тогда, по условию задачи n=5 и k=3:

$\displaystyle C_{5}^{3} =\dfrac{5!}{3! \cdot (5-3)!}=\dfrac{1 \cdot 2\cdot 3\cdot 4\cdot 5}{1\cdot 2\cdot 3\cdot 2!}=\dfrac{4\cdot 5}{2!}=\dfrac{4\cdot 5}{1 \cdot 2}=2\cdot5=10.$