Скласти рівняння прямої b паралельної до а: 2х – у – 3 = 0 та прямої с перпендикулярної до а, які проходять через точку А( –5;3). Побудувати прямі.
Другие вопросы по теме Математика
Популярные вопросы
- Бенефиций — это земель во владение за службу 2) клятва верности вассала своему...
2 - Установите соответствие между терминами и их значением. К каждой позиции из...
3 - Какое из названных событий произошло раньше всех других? 1) первая экспедиция...
3 - Что из названного относится к деятельности Карла Великого? Выберите два верных...
3 - Установите соответствие между терминами и их значением. К каждой позиции первого...
2 - Дополните недостающие названия, выбрав их из приведенного ниже перечня. Основными...
1 - Установите соответствие между именами исторических лиц и родом их деятельности....
3 - Какие две церковные церемонии укреплению власти франкских королей? Запишите...
3 - Какое событие произошло в 476 году? 1) разделение Римской империи на западную...
1 - Салической правдой назывался...
2
Пошаговое объяснение:
для прямой 2х – у – 3 = 0
вектор нормали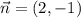
a) прямая параллельная к b
этот же вектор вектор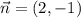 будет нормальным вектором к искомой прямой прямой
будет нормальным вектором к искомой прямой прямой
тогда напишем уравнение прямой, походящей через точку А( –5;3) и имеющей нормальный вектор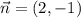
2(x+5) + (-1)(y+3)=0
или
2х -y +13 = 0 - это уравнение прямой b, параллельной прямой
2х – у – 3 = 0 и проходящей через точку А(-5; 3)
б)
вектор нормали прямой 2х – у – 3 = 0 (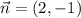 ) будет направляющим вектором исходной прямой
) будет направляющим вектором исходной прямой 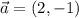
тогда напишем уравнение прямой, походящей через точку А( –5;3) и имеющей направляющий вектор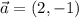
или приведем к общему виду
-(х+5)=2у -6
2у +х -1 = 0 - это и есть уравнение прямой b, перпендикулярной прямой 2х – у – 3 = 0 и проходящей через точку А(-5; 3)