Sin4x+sin7x=cos4x+cos7x В ответе запишите наибольший отрицательный корень уравнения (в градусах) умноженный на 11

-270

Пошаговое объяснение:

Воспользуемся формулами суммы синусов и суммы косинусов:

. При k = 0 , при k = -1 — наибольший отрицательный корень в данной серии.

При n = 0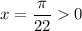 , при n = -1 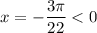— наибольший отрицательный корень в данной серии.

Так как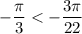 , наибольший отрицательный корень уравнения — 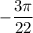. В ответ запишем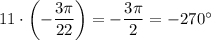

sin4x+sin7x=cos4x+cos7x

В ответе запишите наибольший отрицательный корень уравнения (в градусах) умноженный на 11 .

ответ:   - 180° .

Пошаговое объяснение:  sin4x+sin7x=cos4x+cos7x  ⇔

(sin4x - cos4x) + (sin7x - cos7x) = 0  ⇔√2 sin(4x -π/4) +√2 sin(7x -π/4) ⇔

√2 *2sin(11x/2 - π/4)*cos(11x/2) =0       || 2√2≠0 ||  ⇔

[sin(11x/2- π/4)=0 ; cos(11x/2)= 0.(совокупность уравнений в одной строке)

[11x/2 - π/4 =πk  ;  11x/2 = π/2 +πn   k , n  ∈ ℤ .

[11x/2  = -3π/4  ;  11x/2 = - π/2  при   k=n= -1  ∈ ℤ .

* * *  максимальные отрицательные  корни уравнений   * * *

[11x  = -3π/2  ;  11x = - π  при   k=n= -1  ∈ ℤ  ⇔

[x = -3π/22 ;  x = - π/11  при   k=n= -1  ∈ ℤ

Максимальный отрицательный  корень уравнения  x = - π /11

11x= - π  = - 180°

* * *  sinα + sinβ = 2sin( (α + β)/2 ) *cos( (α - β)/2 )       * * *