1. Математика
  2. Sin x/2 = -1 tg(2x-п/4) = 1 2

Sin x/2 = -1 tg(2x-п/4) = 1 2 sin^2 x=1+cosx sin^2 x-5sinx*cosx+4cos^2x=0 cos2x+cosx=0 cпасибо большое заранее.

abuovalmaz69 abuovalmaz69    1   26.09.2019 15:50    0

Ответы
Аля2011 Аля2011  16.08.2020 22:35
K∈Z (k - любое целое число)
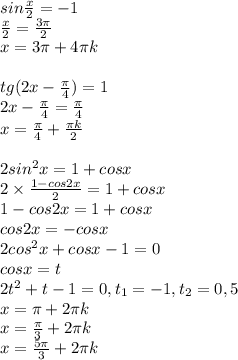
sin \frac{x}{2} =-1 \\ \frac{x}{2}= \frac{3 \pi }{2} \\ x=3 \pi +4 \pi k \\ \\ tg(2x- \frac{ \pi}{4} )=1 \\ 2x- \frac{ \pi }{4}= \frac{ \pi }{4} \\ x= \frac{ \pi }{4} + \frac{ \pi k}{2} \\ \\ 2sin^2x=1+cosx \\ 2\times \frac{1-cos2x}{2} =1+cosx \\ 1-cos2x=1+cosx \\ cos2x=-cosx \\ 2cos^2x+cosx-1=0 \\ cosx=t \\ 2t^2+t-1=0, t_1=-1, t_2=0,5 \\ x= \pi +2 \pi k \\ x= \frac{ \pi }{3} +2 \pi k \\ x= \frac{5 \pi }{3}+2 \pi k
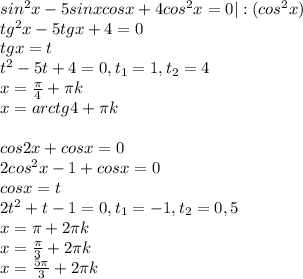
sin^2x-5sinxcosx+4cos^2x=0 | : (cos^2x)\\tg^2x-5tgx+4=0 \\ tgx=t \\ t^2-5t+4=0, t_1=1, t_2=4 \\ x= \frac{ \pi }{4}+ \pi k \\ x=arctg 4 + \pi k \\ \\ cos2x+cosx=0 \\ 2cos^2x-1+cosx=0 \\ cosx=t \\ 2t^2+t-1=0, t_1=-1, t_2=0,5 \\ x= \pi +2 \pi k \\ x= \frac{ \pi }{3} +2 \pi k \\ x= \frac{5 \pi }{3}+2 \pi k
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Vymnuk228 Vymnuk228  11.06.2020 13:05
Решите уравнение: 7 tg x + cos^2 x + 3 sin 2x = 1...
vuqar203 vuqar203  11.06.2020 13:05
учитель поставил половине класса двойки .троек он поставил на 6 меньше чем двоек. четверок на 3 меньше чем троек.а пятерок в двое меньше чем четверок сколько учеников писали контрольную...
мем23 мем23  11.06.2020 13:05
6. Шебер 4 күнде 3 жұп аяқ киім жасайды, ал оның шәкірті 6 күнде 2 жұп аяқ киім жасайды. Екеуі бірігіп, олар 65 жұп аяқ киімді қанша күнде бітіреді? Можно ответ...
lailasarsenbaev lailasarsenbaev  11.06.2020 13:08
На разные клетки шахматной доски произвольным образом поставили две ладьи (белую и чёрную). Что вероятнее: окажутся ладьи под ударом друг друга или нет?...
Лейла5225 Лейла5225  11.06.2020 13:09
4 Гипербола, задана уравнением х2-4y2=16. Найти фокусы, эксцентриситет, составить уравнения асимптот 5 Определить центр и радиус окружности x2+y2-8x=0 6 Составить уравнение параболы,...
Anutka87igorevna Anutka87igorevna  11.06.2020 13:09
Мына реакциялардына алмак ан амтдерін түр түм бардак пен амандер одерни прарынан сімен әсер еткенде онышп шыгуынын русастығын дәлелдетитемдеугсралтындар2 Каныккан катардағы аромат...
VankaOchevidnost135 VankaOchevidnost135  11.06.2020 13:09
Найдите объём многогранника вершинами которого являются точки , ,, правильной треугольной призмы , площадь 11 111 основания которой рана 4, а боковое ребро равно 3....
Lenaclati Lenaclati  12.06.2020 13:13
За 3 часа машина привезла 321 кг сладостей. Сколько она привезет за 8 часов, если будет двигаться с той же скоростью? P.s. можно только ответ...
katyvolkova81 katyvolkova81  11.06.2020 13:18
Даю все что есть нужно решить...
Полинаhelpme1 Полинаhelpme1  11.06.2020 13:18
Найдите первоначальную функцию, проходящую через точку М(2; -10) функции f(x) = ех – 2 + 4х...

Популярные вопросы