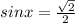Sin^2x cosx+2sin^2x-0,5cosx-1=0
Другие вопросы по теме Математика
Популярные вопросы
- Виктория озеро определение, происхождение 5 класс ответь...
1 - :какой объем (н.у) занимает этиламин,масса которого 22г....
2 - Рамында 40% күкірт және 60% оттек бар қосылыстың формуласын анықтаңдар...
1 - Напишите предложение по с моей мамой...
3 - Периметр четырехугольника равен 42 см, а две его стороны равны 10 и 18 см. найдите...
2 - Как решить пример 879*170/34+2830*47/282 по действиям?...
2 - Сделайте текст из этих слов advise advice person personal host hostess move rule...
3 - Чи проходить графік вункції y=4^x через точку а, якщо: 1)а(4; 16); 2)а(4; 256);...
3 - Дано: четырех угольная правидная пирамида основания является ромб.диогоналами...
3 - Казахский язык 3 класс рабочая тетрадь, урок 8 2....
1
Пошаговое объяснение:
sin²x*cosx+2sin²x-0,5cosx-1=0
(sin²x*cosx-0,5cosx)+(2sin²x-1)=0
cosx*(sin²x-0,5)+2*(sin²x-0,5)=0
(sin²x-0,5)*(cosx+2)=0
sin²x-0,5=0 или cosx+2=0
sin²x=0,5 или cosx= - 2, -2∉[-1;1], => решений нет
1.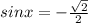
2.