Середнє арифметичне двох чисел дорівнює 28 . знайти менше з них якщо 12,5% одного становить 5 % другого

Question

Математика: Середнє арифметичне двох чисел дорівнює 28 . знайти менше з них якщо 12,5% одного становить 5 % другого

3231561 · Answer

Переводимо в десяткові дроби, 12.5% = 12.5%/100% = 0.125 і 5%=0.05

Нехай х - коефіцієнт пропорційності, тоді перше число дорівнює 0.125x, а друге - 0.05x. Середнє арифметичне двох чисел дорівнює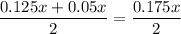 $\dfrac{0.125x+0.05x}{2}=\dfrac{0.175x}{2}$ , що за умовою задачі становить 28, складаємо рівняння:

$\dfrac{0.175x}{2}=28\\ \\ 0.175x=28\cdot 2\\ \\ 0.175x=56\\ \\ x=56:0.175\\ \\ x=320$

Значить маємо такі числа: 0.125 * 320 = 40 і 0.05*320 = 16.

Другий б.

Нехай перше число дорівнює x , тоді друге - у. Їх середнє арифметичне -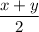 $\dfrac{x+y}{2}$ , що за умовою становить 28. Відомо, що 12,5% одного становить 5% другого, тобто 0.125x = 0.05y, складаємо систему рівнянь

$\displaystyle \left \{ {{\dfrac{x+y}{2}=28} \atop {0.125x=0.05y~~|:0.05}} \right.~~~\Rightarrow~~~\left \{ {{x+y=56} \atop {y=2.5x}} \right.\\ \\ 2.5x+x=56\\ \\ 3.5x=56\\ \\ x=56:3.5\\ \\ x=16\\ \\ y=2.5\cdot16=40$