Сделайте с решением, если понравится отмечу как лучший
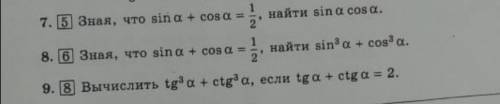
Другие вопросы по теме Математика
Популярные вопросы
- КТО ШАРИТ В ЯДЕРНОЙ ФИЗИКЕ Какой химический элемент содержит 35...
2 - Таємне товариство боягузів ,або засіб від переляку 9 Що ти думаєш...
1 - Не решая уравнение x2+5x+3x+120=0, определи, имеет ли оно корни....
3 - Разность квадратов корней уравнения x^2 – 8x + c = 0 равна 32....
2 - Дано, что ΔCBA — равнобедренный.Основание BA треугольника равно...
3 - Задание 2. Перечислите отличительные особенности семействкласса...
2 - 1. Выбери нужное слово. Запиши предложение. 1) We haven t got much...
1 - 1.Жанр произведения Л. Пантелеева «Честное слово».А) сказка;Б)...
2 - Надо выбрать правильный предлог. Are you interested for/in going...
3 - Выполнить синтаксический и пунктуационный разбор предложений. 1....
1
7. -3/8
8. 11/16
9. 10
7. используем формулу квадрат суммы ( a+b)²=a²+2ab+b² и основное тригонометрическое тождество sin² α+cos² α=1
8. используем формулу сумма кубов, и решения из номера 7
sin³α+cos³α=(sin α+cos α)(sin² α - sin cos α+cos² α)=
9. tg³ α + ctg³ =(tg α+ctg α)(tg²- tgα *ctg α +ctg² α)=
=(tg α+ctg α)(tg²- tgα *ctg α +ctg² α -- tgα *ctg α+ tgα *ctg α)=
=(tg α+ctg α)(tg²- 2tgα *ctg α +ctg² α + tgα *ctg α)=
=(tg α+ctg α)((tg α+ctg α)²+ tgα *ctg α)=2*(2²+1)=10