сам вообще не не справлюсь
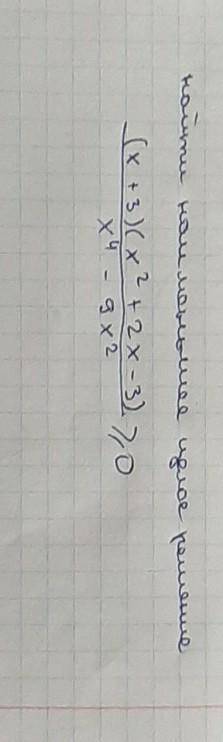
Другие вопросы по теме Математика
Популярные вопросы
- Лайт во какого цвета шерсть у вашей кошки интересно:...
3 - Найти: расстояние от точки А до прямой (рис. 4.347) Найти: расстояние от...
1 - Что относится к выплаченным трансфертам? Укажите один или несколько правильных...
2 - Әлемдегі ең ауыр кітап –Лондондағы Британ мұражайында сақтаулы тұрған географиялық...
1 - Два контура связаны индуктивно и настроены на частоту 5 МГц. Коэффициент...
2 - Местоимение которое может быть притяжательным и личным...
2 - Написати твір-роздум на тему Чи варто за будь-яку ціну добиватися своєї...
1 - Описать магний с точки зрения проявлять окислительно-восстановительные...
3 - Укажите войну,причиной которой являлись религиозные противоречия.Семилетняя,Северная,Тридцатилетняя....
3 - 1. Невесомый рычаг, представленный нарисунке, под действием сил F²=40 Н...
2
Смотри....................................
Пошаговое объяснение:
((x+3)(x²+2x-3))/(x⁴-9x²)≥0, где x⁴-9x²≠0; (x²-3x)(x²+3x)≠0
x²-3x≠0; x(x-3)≠0; x≠0; x≠3
x²+3x≠0; x≠0; x≠-3
Допустим:
((x+3)(x²+2x-3))/(x⁴-9x²)=0
x+3=0; x=-3 - этот корень не подойдет, так как x≠-3.
x²+2x-3=0; D=4+12=16
x₁=(-2-4)/2=-6/2=-3 - этот корень не подойдет, так как x≠-3.
x₂=(-2+4)/2=2/2=1
При x<-3: ((-5+3)(25-10-3))/(625-9·25)≥0; (-8·12)/(625-225)<0 - неравенство не выполняется.
При -3<x<0: ((-2+3)(4-4-3))/(16-36)≥0; -3/(-20)≥0; 3/20>0 - неравенство выполняется.
При 0<x≤1: ((1+3)(1+2-3))/(1-9)≥0; 0=0 - неравенство выполняется;
((1/2 +3)(1/4 +1-3))/(1/16 -36)≥0; (7/2 ·(-7/4))/(-35 15/16)≥0; (49/8)/(35 15/16)>0 - неравенство выполняется.
При 1≤x<3: ((2+3)(4+4-3))/(16-36)≥0; (5·5)/(-20)<0 - неравенство не выполняется.
При x>3: ((5+3)(25+10-3))/(625-225)≥0; (8·32)/(625-225)≥0 - неравенство выполняется.
Отсюда следует: (-3<x<0)∨(0<x≤1)∨(1≤x<3)∨(x>3).
Следовательно, x∈(-3; 0)∪(0; 1]∪(3; +∞).