с задачей на теорию вероятности!
Другие вопросы по теме Математика
Популярные вопросы
- В каком городе родился Чуковский?...
2 - Сочинение на тему весна тип текста описание ...
3 - Какой из видов торговли на казахской земле имел особый приоритет, выясните...
1 - Ширина прямоугольника равна 75 см что составляет 3/5 длины Найдите площадь...
2 - сделать упражнение 3 по русскому Упражнение 3: Напишите продолжение сказки....
3 - Task-1. Open the brackets using the Past Simple or Past Continuous Tenses....
1 - Суретке қара.Берілген мәліметті қоолданып,әңгіме құрап айт. ...
2 - Упростите выражение( 2х -1) ( 4х²+2х+1)- 4х( 2х²-3):...
2 - Из нижеприведенного перечня выберите свойства, характерные для веществ...
1 - Найди: 1+2+22+...+2151+2+22+...+27 . ответ: 1. в решении задачи используется...
3
A - вытащена катушка белого цвета. p(A)=0,4
а) По формуле Бернулли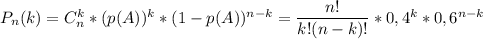
б)
Аналогично ищем по формуле Бернулли при k=2, 3, 4, а затем ищем сумму: