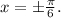с тригонометрическим уравнением
Другие вопросы по теме Математика
Популярные вопросы
- Бір сағатта неше градус өтеді...
3 - Если расстояние 5км а время 10ч какое скорость...
2 - Выпуск продукции предприятия составляет 12 тыс. изделий в год. В состав...
1 - 1) Какие факторы оказывают влияние на климат Сурхандарьинского физико...
3 - Choose the correct variant. 1. A few kinds of shoes 2. Much sacks...
1 - X²+y²-2(y+4x)+17≥0 Довести что при любом значении сменных:...
2 - Стихійні лиха. Правила поведінки під час сильного вітру, грози та...
3 - Написать программу на алгоритмическом языке. В которой: - даны две...
3 - РЕШИТЬ ЗАДАЧУ отрезок A1B1 ортогональная проекция отрезка AB к плоскости...
1 - How many meals have you got a day? What advice can you recommend to...
3
4
Пошаговое объяснение:
Данное уравнение равносильно совокупности:
Первое уравнение дает корни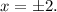
Решим уравнение системы:
Решением неравенства системы является отрезок![x \in [ - 2;\,\,2].](/tpl/images/4978/3998/aae71.png) Таким образом, из множества решений уравнения надо выбрать только те корни, которые принадлежат этому отрезку. Несложно убедиться, что туда попадают только
Таким образом, из множества решений уравнения надо выбрать только те корни, которые принадлежат этому отрезку. Несложно убедиться, что туда попадают только