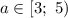с решением, желательно с пояснением. В ответах указано А {3} U [4;5)

Другие вопросы по теме Математика
Популярные вопросы
- Радиус сферы шара равен2,6 дм. найдите длину линии пересечения...
3 - Дана правильная пирамида в основании квадрат со сторонами 16см,...
1 - 1)что такое экология? 2)почему нужно беречь неисчерпаемые ресурсы?...
1 - 1)3=4(x+2) 2)-7=5(x+5) 3)9=5(x+9) 4)7(x-1)=3x 5)9(x+7)= -x 6)5(x-3)=4x...
1 - 1) what do you think happened when they went home? listen and...
3 - I. раскройте скобки, заменяя инфинитив нужной формой глагола-сказуемого....
3 - Материальная точка движется прямолинейно по закону s(t)=t^3-12t^2+60t(s-...
2 - Лестница соединяет точки а и в и состоит из 20 ступеней.высота...
1 - Запиши текст задчи, которой записана с уравнения : х+(х-3)+2(х-3)=89...
1 - Уфігурі закресли 2 відрізки,щоб залишилося 4 рівних квадрати...
3
Рассмотрим две функции:
Изобразим данные функции на координатной плоскости.
Чтобы построить график функции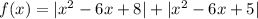 , следует раскрыть модуль на участках.
, следует раскрыть модуль на участках.
Найдем нули модулей функции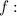
Рассмотрим функцию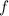 на пяти участках и раскроем модули в соответствии с участком (см. таблицу), используя правило:
на пяти участках и раскроем модули в соответствии с участком (см. таблицу), используя правило:
Построим график функции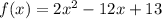 на участке
на участке 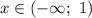 (см. пункт
(см. пункт 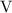 )
)
Построим график функции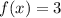 на участке
на участке ![x \in[1; \ 2]](/tpl/images/1356/5780/1fbb1.png)
Пересечение с осями координат:
1) с осью абсцисс: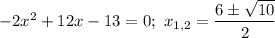
2) с осью ординат: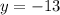
Построим график функции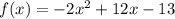 на участке
на участке ![x \in[1; \ 2]](/tpl/images/1356/5780/1fbb1.png)
Построим график функции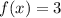 на участке
на участке ![x \in[4; \ 5]](/tpl/images/1356/5780/b98d5.png)
Построим график функции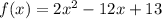 на участке
на участке 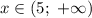
Пересечение с осями координат:
1) с осью абсцисс: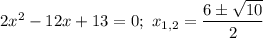
2) с осью ординат: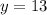
Изобразим график функции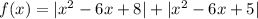 (см. рисунок).
(см. рисунок).
Уравнение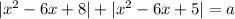 будет иметь более трех решений, если прямая
будет иметь более трех решений, если прямая 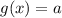 будет иметь более трех точек пересечения с графиком функции
будет иметь более трех точек пересечения с графиком функции 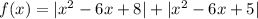
Изобразим возможные варианты решений (см. рисунок).
1) Если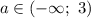 , то уравнение не имеет решений.
, то уравнение не имеет решений.
2) Если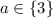 , то уравнение имеет множество решений (промежуток решений).
, то уравнение имеет множество решений (промежуток решений).
3) Если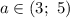 , то уравнение имеет 4 решения.
, то уравнение имеет 4 решения.
4) Если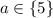 , то уравнение имеет 3 решения.
, то уравнение имеет 3 решения.
5) Если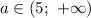 , то уравнение имеет 2 решения.
, то уравнение имеет 2 решения.
Таким образом, при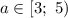 уравнение
уравнение 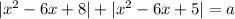 имеет более трех решений.
имеет более трех решений.
ответ: