с решением любого задания, желательно 2 части


Другие вопросы по теме Математика
Популярные вопросы
- Установи правильную последовотельнасть увелевения разнообразия...
1 - Прокоментуйте реплік князя й пустельника в діалозі: -Певно,...
1 - , мне завтра сдавать Известно:МВ||АКМТ=РКугол МТВ=углу КРАДОКОЗАТЬ:...
3 - Обчисліть силу струму напругу та спожиту потужність якщо опори...
2 - Английский язык. 3-класс. стр 82. упражнения 6...
1 - Поясніть чому пустельник не хотів учити дракона читати? Що ознаають...
1 - Інгарії побутує думка що народитися найстаршим у сім ї це...
1 - УКР МОВА складіть і запишіть по два речення з словами здається...
1 - Билет №16. Условия плавания тел. Использование условий плавания...
2 - Найдите сумму целых чисел-решение неравенства: log1/3(2+3x)≥-3...
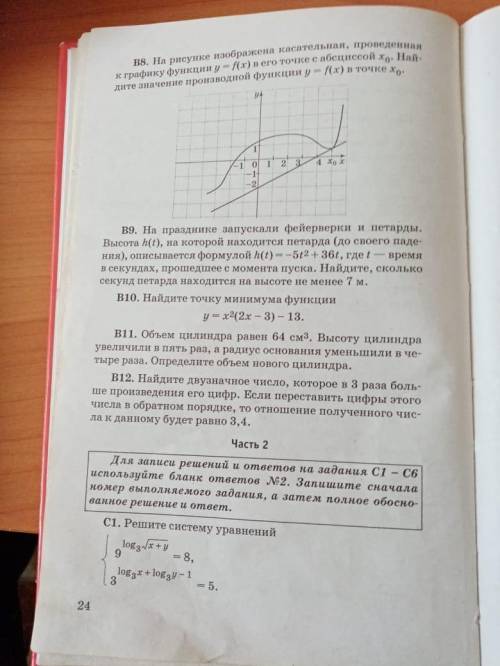
2
Пошаговое объяснение:
C1) ОДЗ: x>0, y>0
преобразуем 1-е уравнение, (V-корень)
3^2log3 V(x+y)=8, 3^log3 (x+y)=8, x+y=8,
преобразуем 2-е ур-е, 3^log3 x *3^log3 y *1/3=5,
x*y*1/3=5, xy=15,получили два простых уравнения, которые решаются
подбором, х=3, у=5 или х=5, у=3, отв. (3;5), (5;3)
С3) ОДЗ: x-4>=0, x>=4 и x не=5,
введем переменную V(x-4) =t, t>=0, тогда при возведении
обеих частей, получим: х-4=t^2, x=t^2+4, x-5=t^2+4-5=t^2-1, тогда,
( (t^2+4-4)*t +1)/(t^2-1)<(t+2), ( (t^3+1)/(t^2-1)-(t+2)<0,
(t^3+1-(t^2-1)*(t+2)) /(t^2-1)<0, (t^3+1-t^3-2t^2+t+2) /(t^2-1)<0,
(-2t^2+t+3)/(t^2-1)<0, (2t^2-t-3)/(t-1)(t+1)>0, D=1+24=25, t1=1,5, t2=-1,
2(t-1,5)(t+1)/(t-1)(t+1) >0, решим методом интервалов,
+___(-1)___+___(1)-(1,5)+___ , t>=0,
0<=t<1 и t>1,5, обратная замена 0<= V(x-4)<1 , 0<=(x-4)<1, 4<=x<5
и V(x-4)>1,5, x-4>2,25, x>6,25, ответ: [4;5), (6,25; +Б)