С ПРИМЕРОМ

Найдите площадь фигуры, ограниченной линиямиy=2-x^2 и y=1

Ответы

ktotoipotom 15.10.2020 13:02

Решение:

Приравняем функции и решим полученное квадратное уравнение:

$2-x^2=1 \\ \\ -x^2=-1 \\ \\ x=\pm \sqrt{1} \\ \\ x=\pm 1$

По формуле Ньютона-Лейбница найдём площадь нашей фигуры:

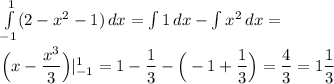
$\int\limits^1_{-1} (2-x^2-1) \, dx = \int\limits 1 \, dx - \int\limits x^2 \, dx = \\ \\ \Big(x -\dfrac{{x}^{3}}{3}\Big)|^1_{-1}=1-\dfrac{1}{3}-\Big(-1+\dfrac{1}{3}\Big)=\dfrac{4}{3}=1\dfrac{1}{3}$

ответ: $\sf S=1\dfrac{1}{3}$
С ПРИМЕРОМ Найдите площадь фигуры, ограниченной линиямиy=2-x^2 и y=1

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика

natvasilya16 15.05.2020 22:23

с матешом написала равно, а че дальше я хз...

орионер 15.05.2020 22:23

Катер пливе за течією на1,1 Угод більше ніж проти течії і подолав загальний шлях 103 кілометрів скільки часу він витратив на всю дорогу туди і назад якщо швидкість...

istamov9777 15.05.2020 22:23

сколько будет 99658%/567%...

roma280274 15.05.2020 22:23

В каком классе проходят асимптоты?...

gei228 15.05.2020 22:23

Наименьший делитель числа, отличный от 1, будем называть минимальным. Наибольший делитель числа, отличный от самого числа, будем называть максимальным. Найдите четырёхзначное...

SQQQUAD 15.05.2020 22:23

Https://thriveglobal.com/?p=1386082&preview_nonce=7b720939cd&preview=true...

xandar815 15.05.2020 22:23

У клоуна было 36 шаров, он раздал детям 49 части всех шаров. СКОЛЬКО ШАРОВ ОСТАЛОСЬ У КЛОУНА...

Matrixx666 15.05.2020 22:24

Розв яжи задачу рівнянням. Автобус за три дні пройшов 2200 км. першого дня він пройшов 32% всього шляху, а другого на 88 км більше, ніж третього. Який шлях проходив...

denjis 15.05.2020 22:24

Кути трикутника дорівнюють 35° ; 42° ; 103°. Як називається такий трикутник?...

sanyok505 12.12.2020 05:30

Балықшы екі балық аулап алды. Бірінші балықтың массасы KI10ал екінші балық оданк жеңіл. Барлығы неше килограмм.балық аулап алды? бұл бжб...

С ПРИМЕРОМ Найдите площадь фигуры, ограниченной линиямиy=2-x^2 и y=1

Популярные вопросы

С ПРИМЕРОМ

Найдите площадь фигуры, ограниченной линиямиy=2-x^2 и y=1