1. Математика
  2. С объяснением . Найти пределы,

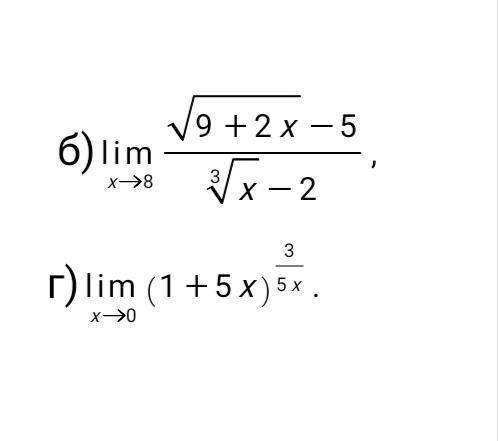
С объяснением . Найти пределы, не применяя дифференциальное исчисление (правило Лопиталя):


С объяснением . Найти пределы, не применяя дифференциальное исчисление (правило Лопиталя):

Scipelex76 Scipelex76    3   25.01.2022 19:48    0

Ответы
ilonabagdasarya1 ilonabagdasarya1  25.01.2022 19:50

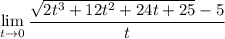б) Сделаем замену (только для удобства) \sqrt[3]{x} = t+2. Тогда предел перепишется в виде \lim\limits_{t\to 0}\dfrac{\sqrt{2t^3+12t^2+24t+25}-5}{t}. Поскольку 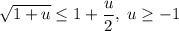\sqrt{1+u} \leq 1+\dfrac{u}{2},\; u\geq -1 (докажите самостоятельно), то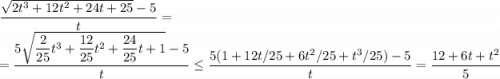 \dfrac{\sqrt{2t^3+12t^2+24t+25}-5}{t}=\\ = \dfrac{5\sqrt{\dfrac{2}{25}t^3+\dfrac{12}{25}t^2+\dfrac{24}{25}t+1}-5}{t}\leq \dfrac{5(1+12t/25+6t^2/25+t^3/25)-5}{t} = \dfrac{12+6t+t^2}{5}

С другой стороны, можем умножить и разделить дробь на сопряженное: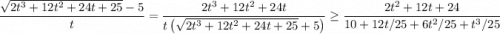 \dfrac{\sqrt{2t^3+12t^2+24t+25}-5}{t} = \dfrac{2t^3+12t^2+24t}{t\left(\sqrt{2t^3+12t^2+24t+25}+5\right)}\geq \dfrac{2t^2+12t+24}{10+12t/25+6t^2/25+t^3/25}

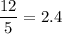В итоге получили \dfrac{12}{5}\stackrel{t\to 0}{\leftarrow}\dfrac{2t^2+12t+24}{t^3/25+6t^2+12t/25+10}\leq\dfrac{\sqrt{2t^3+12t^2+24t+25}-5}{t}\leq \dfrac{12+6t+t^2}{5}\stackrel{t\to0}{\to} \dfrac{12}{5}, следовательно искомый предел равен \dfrac{12}{5} = 2.4.

г) \lim\limits_{x\to 0}(1+5x)^{\frac{3}{5x}} = \left[\lim\limits_{x\to 0}(1+5x)^{\frac{1}{5x}}\right]^3 = \left[e\right]^3 = e^{3}.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Sazon1000 Sazon1000  07.11.2019 17:27
Артем рисует в клетчатой тетради фигуры тетрамино . эти фигуры состоит из 5 клеточек и у каждой клеточки есть хотя бы одна общая страна с другой клеточкой. сколько всего различных...
asylzhan1977 asylzhan1977  07.11.2019 17:26
Ыражения 44,2b-(15,8b+23,45) при b=1,7....
lina5555555 lina5555555  07.11.2019 17:25
Поливная площадь нашей школы занимает 1100м2, первый день полили 9/25 всей этой площади, а второго 15/32 решти.обчислить площадь, осталась политой....
sonikzets sonikzets  07.11.2019 17:22
56/69 умножить на 66/77 с объяснением ,...
shulyakovatati shulyakovatati  07.11.2019 17:22
[tex]2 \cos (\frac{\pi}{3} - x) = 1[/tex]...
vasipovismail vasipovismail  07.11.2019 17:22
20 + 40 + 40 + 80 + 80 + 160 + 60 + 230 + 230 + 85 + 350 + 250 + 689 + 35 ​...
няшка366 няшка366  07.11.2019 17:22
Не выполняя вычислений, сравните значения выражений: 1) 123 + 49 и -170 2) -184 + 3 и 184 3)-349 - 76 и 35 4) -512 -120 и -512 5)232 - (-89) и 232 + 89 6) 24 - 345 и -24 + 345...
milenkakonfetka milenkakonfetka  07.11.2019 17:21
Решите 26,28 или какое-то из них 10...
немагистор немагистор  07.11.2019 17:21
40÷1 2 3 4 5=40 скобки и знаки нужно поставить​...
krokodilol krokodilol  07.11.2019 17:20
Решить с условием : масса арбуза-8кг. чему равна масса половина арбуза? б) половина арбуза имеет массу 4кг. чему равна масса всего арбуза? ​...

Популярные вопросы