с математикой. 22 номер все примеры. пошаговое решение.​

Пошаговое объяснение:

a) табличный интеграл = arctgx + C

в подстановке 1__0 получим arctg(1) - arctg(0) = pi/4 - 0 = pi/4

б) занесу 3х + 1 под дифференциал:

d(3x+1) = 3 dx => dx = 1/3 d(3x+1) => 1/3 *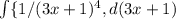   = 1/3 * (-1/3)* 1/(3x+1)^3 + C = -1/(9*(3x+1)^3) + C

в подстановке 1__0 получим -1/(9*4^3) + 1/(9*1^3) = -1/576 + 1/9 = 63/576 = 7/64

в)занесу cosx под дифференциал:

cosx dx = d(sinx)

d(3sinx+1) = 3cosx dx => dx = 1/3cosx * d(3sinx+1)

получим 1/3*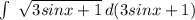   = 1/3 * 2/3 * (3sinx + 1)^(3/2) + C

в подстановке pi/2__0 получим 2/9 * (3+1)^3/2 - 2/9*(1)^(3/2) = 16/9 - 2/9 = 14/9

г) занесу e^(-2x) под дифференциал

d(e^(-2x)) = -2*e^(-2x) dx

dx = 1/(-2*e^(-2x)) d(e^(-2x))

получим: -1/2 *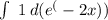 (cтепень криво написалась) = -1/2 * e^(-2x) + C

в подстановке -1/2__0 получим -1/2 * e^(1) + 1/2* e^(0) = 1/2(1 - e)