Розв'яжи рівняння:
1)-х=10
2)-х=-2
3)
4)
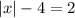
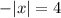
Другие вопросы по теме Математика
Популярные вопросы
- Шаңырақ кереге уық есік үй туралы фразеологизмдер ...
3 - Сравните дроби 3/10 и 4/11; 8/25 и 13/40...
2 - A) найдите прилиженное значение до десятых: 3,052; 0,0876; 0,236.б) найдите...
3 - Роль грибов и бактерий в жизни человека сообщение....
3 - Продемонстрируйте одну из возможностей картографических онлайн сервисов посредством...
3 - Выполнить перевод: 10101011,011101 из двоичной системы в 16ричную...
2 - Abcd параллелограмм p=8√3 угол b=150° r-?...
2 - Масса образца сплава кадмия с медью равна 0,630 кг. плотность сплава свинца...
1 - Синтаксический разбор предложения кошка тыщила маленьких котят за шкирку...
1 - Периметр прямоугольника равен 26см а его площадь 42см найдите координаты...
3
1)-х=10
х= -10
2)-х= - 2
х=2
3)|х|-4=2
|х|=2+4
|х|=6
х=6
х= -6
4)-|х|=4
|х|= -4
-х = 10;
Теперь у нас получилось уравнение с положительным "х", и мы можем выразить его значение:
х = -10.
2) Аналогично предыдущему примеру, здесь нужно найти значение "х", при котором -х будет равно -2:
-х = -2;
Умножаем обе части уравнения на -1:
х = 2.
3) Данное уравнение имеет вид |х| - 4 = 2. Здесь важно понимать, что выражение |х| означает абсолютное значение числа "х", которое всегда будет положительным значением.
Для решения уравнения с абсолютным значением, мы можем разделить его на два случая:
1. Когда х положительно, выражение |х| равно просто х:
х - 4 = 2;
Добавляем 4 к обеим частям:
х = 6.
2. Когда х отрицательно, абсолютное значение |х| равно -х:
-х - 4 = 2;
Добавляем 4 и умножаем обе части на -1:
-х = -6;
Делим обе части на -1:
х = 6.
Итак, у нас есть два возможных решения: х = 6.
4) В данном уравнении имеется выражение - |х|. Здесь тоже имеются два случая:
1. Когда х положительно, абсолютное значение |х| равно х:
-х = 4;
Умножаем обе части уравнения на -1:
х = -4.
2. Когда х отрицательно, абсолютное значение |х| равно -х:
-(-х) = 4;
Двойной минус превращается в плюс:
х = 4.
Итак, у нас есть два возможных решения: х = -4 или х = 4.