Розв’яжіть диференціальні рівняння
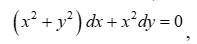
Другие вопросы по теме Математика
Популярные вопросы
- При переводе в ,например, 150см2 (сантиметров квадратных) в м2(метры...
1 - Синтаксического разбора предложения.: он стоял и смотрел, как убивали...
2 - Первьй ехал со скоростью 200 м/мин ,а второй проезжал в минуту на...
1 - Осевое сечение конуса-равнобедренный прямоугольный треугольник,...
3 - Нарисуйте картину линий магнитной индукции при протекании тока через...
1 - Ввазе 10 конфет, 6 шоколадок, 4 карамелек. с какой вероятностью...
3 - На маслозаводі за один день виготовили 16 бочок масла,а за другий-19...
1 - Определить массу, импульс и энергию фотона видимого света с длиной...
1 - Какие герои рассказа а и солженицына один день ивана денисовича...
1 - Велосипед,выпишите первое предложение подчеркните орфограммы и словах,укажите...
2
линейное ДУ
Замена:
общее решение