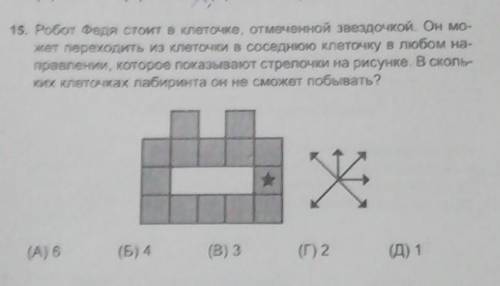
Робот Федя стоит в клеточке, отмеченной звездочкой. Он мо- жет переходить из клеточки в соседнюю клеточку в любом на-
правлении, которое показывают стрелочки на рисунке. В сколь-
ких клеточках лабиринта он не сможет побывать?
(А) 6
(Б) 4
(В) 3
(Г) 2
(Д) 1
Другие вопросы по теме Математика
Популярные вопросы
- А1.какие структурные компоненты входят в состав нуклеотидов молекулы рнк? 1)...
2 - Ввести номер месяца и вывести название времени, язык си...
3 - Автомобиль движется со скоростью 72 км/ч. определить ускорение автомобиля, если...
2 - Расписание по фазам фабричной аварии...
2 - Напишите уравнения реакций получения всех возможных солей( средней, кислых,...
1 - Найти область определения функции y=ln(x+2)+ln(x-2). : )...
1 - Какие три из перечисленных районов располагаются за северным полярным кругом?...
2 - Чем отличается стихотворение от мифа ?...
1 - Раняя осень чудесная не повторимая пора года синтактический разбор...
3 - Знайти область визначення у=2х+1/х²-6...
3
На рисунке видно, что робот может переходить только по стрелочкам, иначе говоря, он не может перепрыгивать через клеточки, которые не соединены стрелками.
Чтобы определить, в каких клеточках робот не сможет побывать, мы можем заполнить лабиринт, начиная с клеточки, в которой стоит робот Федя.
После того, как мы заполним лабиринт, нас интересуют только те клеточки, которые остались незаполненными.
Давайте посмотрим на изначальный вид лабиринта и как мы можем заполнять клеточки:
```
●
↑│→
○↓
```
Мы начинаем с клеточки, в которой стоит робот Федя, и помечаем её как заполненную:
```
■
↑│→
○↓
```
Теперь робот может перейти в клеточки, которые соединены стрелочками с уже заполненными клеточками. Первым ходом у нас есть два варианта - пойти вправо или пойти вниз:
Если робот пойдёт вправо:
```
■
↑│■
○↓
```
Теперь робот может пойти только влево (вверх не может, так как клеточка наверху уже заполнена, а вправо и вниз можно, но это не поможет рассмотреть все клеточки лабиринта):
```
■
←│■
●↓
```
Теперь, когда робот снова вернулся в исходную клеточку, мы отмечаем эту клеточку как заполненную.
Теперь рассмотрим второй вариант, когда робот Федя пойдёт вниз:
```
■
↑│→
●↓
```
Отмечаем следующую клеточку как заполненную:
```
■
↑│→
■↓
```
И снова робот вернулся в исходную клеточку. Теперь у нас уже осталась только одна клеточка, в которую робот не сможет попасть:
```
■
↑│→
■↓
```
Из этого решения видно, что в лабиринте робот Федя не сможет побывать в одной клеточке.
Таким образом, ответ на вопрос задачи: (Д) 1.