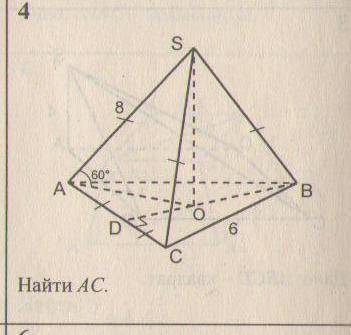
Решите задачу по стереометрии
Другие вопросы по теме Математика
Популярные вопросы
- Ключевые слова стихотворения Листок...
2 - Вертикально розташована пружина з’єднує два вантажі у формі куба. Маса верхнього...
3 - Прочитайте текст. Определите стиль и подстиль текста. Выделите 2 подтемы, озаглавьте...
3 - Знайдіть кути чотирикутника ABCD, ADB=43°, ACD=37°, CAD=22°...
2 - Укажите предложение, в котором НЕ с деепричастием пишется СЛИТНО. Укажите правильный...
1 - Определите виды аббревиатур. ЧП, ООО, ОАО, МОН, МВФ, ООН, СБУ, ПАСЕ, Минфин, ГОСТ...
3 - Потрібно скласти слово,у якому 15 літер,але у мене є лише 13, можливо хтось знає...
2 - Споживач купує 12 одиниці блага Х і 116 одиниць блага Y, маючи доход 2200 грн....
1 - По какому правилу мы записали в слове вич(е)пурений букву е?...
3 - Вопрос Что мне делать, когда я оказалась в случае когда я была избита? Кому стоит...
1
Требуется: Найти отношение объемов полученных частей трехгранного угла ABC.
Решение:
1. Найдем объем всего трехгранного угла ABC. Для этого воспользуемся формулой объема трехгранного угла: V = (AB · BC · AC)/6, где V - объем трехгранного угла, AB, BC и AC - длины его ребер.
В нашем случае AB = 8 см, BC = 5 см, AC - неизвестно. Значит, пока оставим AC в виде переменной.
V = (8 · 5 · AC)/6
2. Теперь найдем объем меньшей части трехгранного угла. Обозначим его V1. Зная, что плоскость проходит через боковую грань трехгранного угла ABC, значит она делит эту грань на две равные части. Примем это равенство ради упрощения решения.
Тогда объем меньшей части угла ABC будет равен половине объема всего угла ABC:
V1 = V/2
Подставляем выражение для V из пункта 1:
V1 = [(8 · 5 · AC)/6]/2
Упрощаем выражение:
V1 = (8 · 5 · AC)/(6 · 2)
V1 = (40 · AC)/12
V1 = (10/3) · AC
3. Теперь найдем объем большей части трехгранного угла. Обозначим его V2. Так как ранее было установлено, что плоскость делит боковую грань на две равные части, то V2 будет также равен V1.
V2 = V1 = (10/3) · AC
4. Наконец, найдем отношение объемов меньшей и большей частей трехгранного угла ABC. Обозначим это отношение как К.
K = V1/V2 = (10/3) · AC / (10/3) · AC
К = 1
Ответ: Отношение объемов меньшей и большей частей трехгранного угла ABC равно 1. Это значит, что объемы этих частей равны между собой.