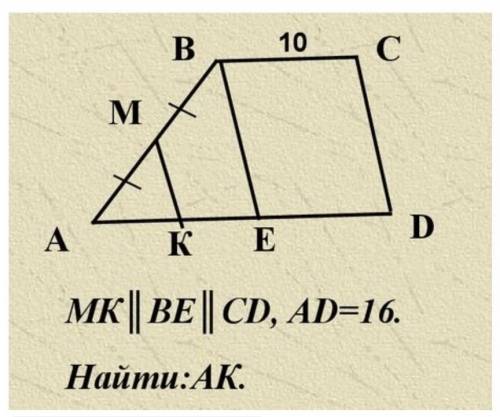
Решите задачу по готовому чертежу ​

Для решения данной задачи нам необходимо найти неизвестное значение x. Внимательно рассмотрим данный чертеж.

На чертеже видно, что данный параллелограмм имеет прямой угол QNM, а сторона QP является диаметром окружностей O1 и O2. Заметим также, что все углы данного параллелограмма равны между собой (см. углы NOP, NOL и NML). Поэтому у нас есть два равных угла NOP и NOL.

Рассмотрим равные углы NOP и NOL. Они образуют основания равнобедренного треугольника PON. Так как NOP = NOL, то угол NOP также равен 40°. Поскольку сумма углов треугольника равна 180°, мы можем найти значение угла PNO: 180° - 40° - 40° = 100°.

Заметим, что угол PNO является центральным углом, опирающимся на диаметр QP окружности O1. Поэтому угол PNO равен половине измеренного дуги QNO, то есть 50°.

Теперь мы можем рассмотреть треугольник QNO. В этом треугольнике, сумма всех углов также равна 180°. Мы уже знаем, что угол QNO = 50°, поэтому уголы QON и QNO равны между собой. Таким образом, угол QON = 50°.

Рассмотрим теперь треугольник QOM. Так как сумма углов треугольника равна 180° и мы уже знаем угол QON = 50°, можем найти угол MOQ: 180° - 50° - 90° = 40°.

Ответ: Угол MOQ равен 40°.