Решите ваша (( 1.а) б)
б) в)
в)) 2.а)
2.а) б)
б)) в)
в)^n)
Другие вопросы по теме Математика
Популярные вопросы
- В Казахстане имеются историко-архитектурные памятники, особый интерес...
3 - Открытый сосуд с углекислым газом уравновесили на весах ...
3 - XV Определите по лентевремениОпределите период прав-ления Тутанхамона.-...
2 - Правильно ли составлена схема индукционного нагревателя?...
1 - Рідинно мозаїчна модель біологічних мембран .чому така будова...
2 - Анализ и нетерпретация текста ЗаданиеПрочитайте отрывок из мифа...
1 - Составь животное на английском из букв ufobalf ...
1 - Содействуют геологической разведке полезных ископаемых и определению...
1 - Казак адебиетинен тоб тоб тоб айтыш...
3 - Соч по Истории казахстана ...
1
Пошаговое объяснение:
1. A)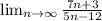
Б)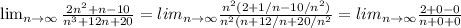 = 2/∞ = 0
= 2/∞ = 0
В) 6/2 + 4/2 = 10/2 = 5