Решите уравнения*** в 213 (***ВАЖНАЯ ПОМЕТКА:Сделали замену и обратно к ней возвращаемся+вычислите дискриминант+уравнение для решения этих* уравнений.(ПРОСБА НЕУДАЛЯТЬ Т.К Я УКАЗАЛ 1 ЗАДАНИЕ¡¡!!)
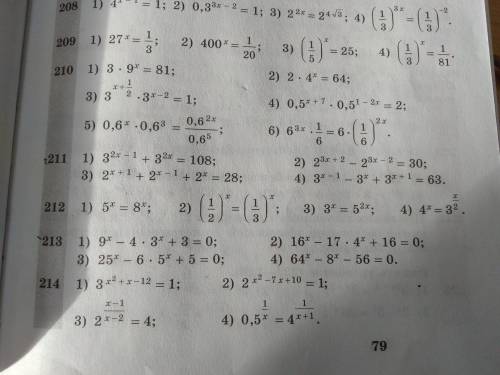
Другие вопросы по теме Математика
Популярные вопросы
- 4,5 так относится к (3х) так как 4 относится 28 это уравнение на тему прямая и...
2 - Выпишите из текста однокоренные слова к словам куры голод...
3 - Ккакой части речи относится слово был...
1 - Найдите периметр прямоугольника если его площадь равна 18см2 а сторона 90 мм...
2 - Выражение 1) 5/8х-1/4х-1/12х+1/6х 2)5/7у+1/4у+3/14у+1 3/4 . заранее ☺...
3 - Мальчик везёт на санках груз прикладовая по направлению движения санок силу 20н...
1 - Слово: непроницаемо ! какая часть и как !...
2 - Как будет хозяин во множественном числе...
2 - Расправила пишется слитно или раздельно...
2 - 3км 865м+7км428м 12км020м-8км350м 8т036 кг- 4т 018кг 1т 200кг- 486кг...
3
1)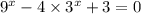
Пусть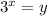 , тогда
, тогда
Подставляем,
ответ: 0; 1
2)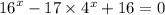
Пусть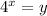 , тогда
, тогда
Подставляем,
ответ: 0; 2
3)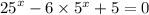
Пусть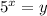 , тогда
, тогда
Подставляем,
ответ: 0; 1
4)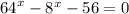
Пусть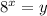 , тогда
, тогда
Подставляем,
положительное число при возведении в степень не может стать отрицательным числом, решения у данного уравнения нет.
ответ: 1