Решите уравнения: 1) 1 + х + х^2 + + х^99 = 0 2) х^2 - 2х^3 + 4х^4 - 8х^5 + = 2х +1, |х|< 1 3) 2х + 1 + х^2 - х^3 + х^4 - х^5 + = 13/6, |х|< 1

1)

Проверим точку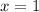 . Равенство не выполняется.

Значит, домножим и поделим на .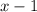

Получим .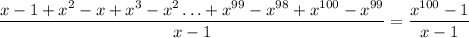

Имеем .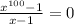

Выражение в числителе над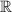 эквивалентно 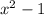, т.к. имеет те же корни .

Значит, единственный корень: .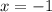

2)

При данных ограничениях решить уравнение невозможно. Сумма слева может расходиться (т.е равняться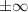 ), ведь знаменатель прогрессии .

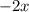Пусть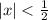

Слева имеем сумму бесконечно убывающей геометрической прогрессии. Значит выражение можно свернуть в:

Или .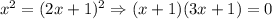

По условию подходит один корень: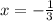

3)

Для простоты преобразуем к виду:

.

Слева сумма бесконечно убывающей геометрической прогрессии.

.

И корни: