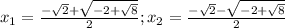Решите уравнение:
x^4+8x-7=0
Другие вопросы по теме Математика
Популярные вопросы
- Анализ стихотворения белая лошадь бредёт без...
2 - Могут ли грибы поселится в воздухе,растении,животном,человеке,в остатках...
2 - 2^3*2^5=2^8; 5^2*5^3=5^5; 2^7*2=2^8; 3^4*3^5*3=3^10;...
1 - Периметр параллелограмма равен 98 см. найдите стороны его стороны, если...
1 - Сочинить сочинение на тему что я должен сделать что бы процветала страна,узбекистан...
1 - Заделать фанатический разбор ямка заранее...
1 - Впечатление три толстяка юрий олеша 15 предложения ...
1 - Сочинение на тему: в чем заключается сила природы ....
2 - Составить план на тему рассказа в.п.астафьева бабушка с малиной ! заранее....
2 - Сделать по ! это надо перевести 12мм квадратных в метры квадратные 21м...
3
x ∈ ∅
ответ: