Решите уравнение
 + 2 log_{(2 - ctgx)}\sqrt{tgx} = \frac{5}{2} )
Другие вопросы по теме Математика
Популярные вопросы
- Some people live in a city where the houses are very tall some people live in the...
1 - Вопрос по языку: стр 58 63 (никитин)...
1 - Какого отношение маши к отцу (дубровский)...
2 - Решите уравнение- -8(x-2) 4-7x...
1 - Cкакими из перечисленных веществ реагирует оксид серы (lv) beo,cl2, o2, naoh ,...
2 - 4класс напишите сочинение на тему субботний вечер у нас дома . расскажите что делают...
1 - Как найти неизвестные сумму,слагаемое,вычитаемое,уменьшаемое,делитель...
2 - Выполните деление г )745 500 000 в столбик не в сокращение...
3 - Как правильно определить у пострадавшего растяжение связок ушибы вывихи...
3 - Найдите значение выражений: a)627 - 46 x 12 + 118 б) 39 x(641 - 5720 : 13) !...
2
Область определения запишем
Систематизируем немного
Из последнего видим, что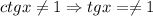 , а это уже есть. Остается тогда
, а это уже есть. Остается тогда
Правда, решая неравенство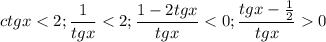
методом интервалов, получаем
Но тангенс из другого неравенства больше нуля, поэтому
Теперь решаем неравенство:
Тут t явно не равно нулю в числителе, поэтому это ограничение нам особо не нужно.
Решаем 1-ое уравнение (t=1/2):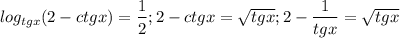
Видно по сумме коэффициентов, равно 0, что p=1 - корень уравнения. Однако,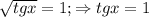 , но по ограничениям не подходит. Теперь делим уголком или по схеме Горнера на p-1 и получаем
, но по ограничениям не подходит. Теперь делим уголком или по схеме Горнера на p-1 и получаем
Видно, что оба значения положительны, но второе и больше 1/2, так как в числителе число, куда больше, чем 1.
А вот другой корень проверим:
Решаем второе уравнение:
(то, что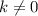 здесь понятно, поэтому смело на него умножаем все уравнение без потери корней)
здесь понятно, поэтому смело на него умножаем все уравнение без потери корней)
Тут сумма коэффициентов равна 0, k=1 - корень. Поделим на k-1 уголком или по схеме Горнера и получим
Корень k=1=tgx нам не подходит, так как по ограничениям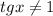
Решаем квадратное уравнение, которое дает нам вторая скобка.
Отрицательный корень не берем, так как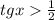
Проверим положительный корень на выполнение ограничений (сравня с 1/2)
Левое выражение больше правого, значит, этот корень удовлетворяет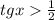 (так как
(так как 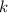 это не целое число, то оно не равно 1, то есть
это не целое число, то оно не равно 1, то есть 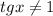 , поэтому корень подходит)
, поэтому корень подходит)
ответ: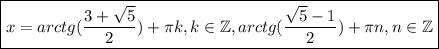
ОДЗ на рисунке (решения долны входить в синие секторы)
решение на фото.