Решите уравнение sin^4 (x)*cos^2 (x) - cos^4(x)*sin^2(x)= cos2x
Другие вопросы по теме Математика
Популярные вопросы
- Чему равна работа силы тяжести при перемещении тела между двумя...
3 - Словообразовательный разбор слова окруженны...
3 - Сколько существует пар двухзначных чисел у которых первое число...
2 - Цену на товар спустили дважды на один и тот же процент. в итоге...
2 - Как работа силы тяжести зависит от формы траектории?...
3 - 18 билет определить вид текста, тему никто точно не знает, когда...
3 - Выполнить умножение: 1. a(х+y) 2. -n(х-y) 3. 3х(х-3)умножить 3х(х-3)...
1 - Свод правил надлежащего исполнения договора...
3 - Заряд, равный 1 нкл, переносится в воздухе из точки, находящейся...
3 - Найти значение выражения : 1) 2b+5a-2b^2/b при а=6,b= - 60 2)...
3
x=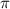 /4+
/4+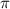 *n/2
*n/2
Пошаговое объяснение:
sin^2(x)*cos^2(x)*(sin^2(x) - cos^2(x)) = cos2x
- sin^2(x)*cos^2(x)*cos2x = cos2x
cos2x + sin^2(x)*cos^2(x)*cos2x = 0
cos2x(1 + sin^2(x)*cos^2(x)) = 0
cos2x = 0 або 1 + sin^2(x)*cos^2(x) = 0
2x =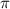 /2+
/2+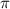 *n або sin^2(x)*cos^2(x) = -1 це неможливо, бо x =
*n або sin^2(x)*cos^2(x) = -1 це неможливо, бо x = 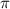 /4+
/4+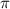 *n/2 квадрати >= 0
*n/2 квадрати >= 0